Агрегатные общие индексы
Объективность общим индексам придает их запись в агрегатном виде, предложенная испанцем Ласпейресом и немцем Пааше.
Агрегатный общий индекс Ласпейреса для количества товаров как первого фактора выручки определяется по формуле
= 
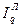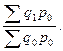(1.75)
Аналогично можно записать агрегатный общий индекс Ласпейреса для цен как первого фактора выручки, то есть
= 
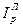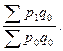(1.76)
В формулах Ласпейреса знаменатели по существу одинаковые, представляя собой выручку базисного периода, а числители разные. В формуле (1.75) это отчетная выручка в базисных ценах (количесгво товаров отчетное, а цены — базисные), в формуле (1.76) наоборот — базисная выручка в отчетных ценах (цены отчетные, а количество товаров — базисное).
Агрегатные общие индексы Пааше применяются ко вторым факторам мультипликативных моделей. Поэтому такой индекс для цен как второго фактора выручки определяется по формуле
= 
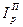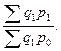(1.77)
Аналогично можно записать агрегатный общий индекс Пааше для количества товаров как второго фактора выручки, то есть
= 
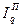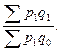(1.78)
В формулах Пааше числители по существу одинаковые, представляя собой выручку отчетного периода, а знаменатели аналогичны числителям формул Ласпейреса.
Для облегчения запоминания студентами формул Ласпейреса и Пааше предлагаю обратить внимание на букву «ш» в слове «Пааше», которая напоминает «111» - так обозначены отчетные периоды в общей формуле (две единицы – в числителе, а одна – в знаменателе). В формуле же Ласпейреса – три нуля (наоборот к формуле Пааше).
Произведения количественного индекса Ласпейреса и ценового индекса Пааше, а также ценового индекса Ласпейреса и количественного индекса Пааше дают общий индекс выручки.
Однако вид этих формул показывает, что однофакторные индексы Ласпейреса и Пааше не равны между собой. То есть не равными являются количественные индексы Ласпейреса и Пааше и ценовые. Американский экономист Гершенкрон обширными расчетами установил, что по одному и тому же фактору индекс Ласпейреса всегда больше индекса Пааше и это открытие названо эффектом Гершенкрона.
Но в статистике должно быть одно значение индекса, поэтому американский экономист Фишер предложил применять среднюю геометрическую величину из индексов Ласпейреса и Пааше, определяя ее по формулам:
для количества товаров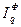 
= 
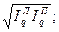(1.79)
для цен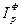 
= 
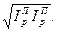(1.80)
Вместе с тем, проведенные Ворониным В.Ф. многочисленные расчеты показали, что для целей статистики вполне можно применять не среднюю геометрическую, а простую среднюю арифметическую величину из индексов Ласпейреса и Пааше, определяя ее по формулам:
для количества товаров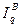 
= 
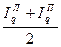(1.81)
для цен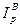 
= 
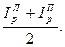(1.82)
Например, если индекс Ласпейреса 1,8 и индекс Пааше 1,4 , то средний геометрический индекс по предложению Фишера равняется
IФ=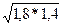 
=1,59,
а средний арифметический индекс по нашему предложению составит
IВ=(1,8+1,4)/2 = 1,60.
Как видим, разница очень незначительная. Но при этом важно во всехпериодах времени постоянно пользоваться одной и той же средней величиной: или геометрической, или арифметической.
Дата добавления: 2015-12-26; просмотров: 1533;