Показательное распределение

Показательным называется распределение вероятностей непрерывной случайной величины 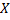, которое описывается плотностью

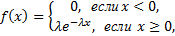
где 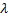- постоянная положительная величина.

Найдём функцию распределения показательного закона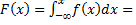

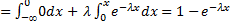. Итак,

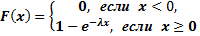
Найдём математическое ожидание = ; .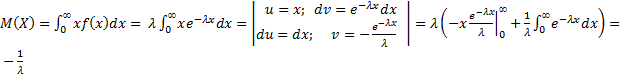

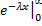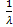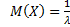Найдём дисперсию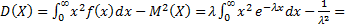

=

= ; ;

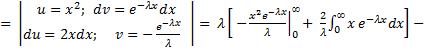
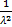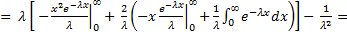
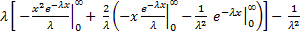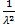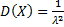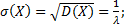
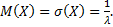
Найдём вероятность попадания в интервал 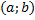непрерывной случайной величины, которая распределена по показательному закону, заданному функций распределения

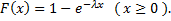
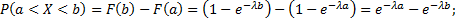
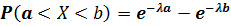
Функция надёжности

Всякое устройство, независимо от того, «простое» оно или «сложное» будем называть элементом.

Пусть элемент начинает работать в момент времени 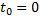, а по истечении времени длительностью 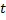происходит отказ. Обозначим через 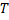непрерывную случайную величину – длительность времени безотказной работы элемента. Если элемент проработал безотказно время, меньшее 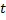, то, следовательно, за время длительностью 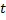наступит отказ. Таким образом функция распределения 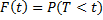определяет вероятность отказа за время длительностью 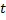. Тогда вероятность безотказной работы за это же время длительностью 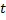, т.е. вероятность противоположного события 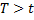, равна .

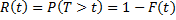Функцией надёжности 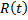называют функцию, определяющую вероятность безотказной работы элемента за время длительностью :

.

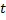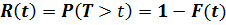Часто длительность времени безотказной работы элемента имеет показательное распределение, функция распределения которого 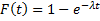. Тогда .

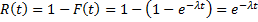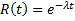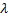Показательным законом надёжности называют функцию надёжности, определяемую равенством , где - интенсивность отказов.