Биномиальный закон распределения (биномиальное распределение) дискретных случайных величин.

Дискретная случайная величина Х распределена по биномиальному закону, если она принимает значения 0,1,2…,m…,n… с вероятностями, которые находятся по формуле Бернулли:

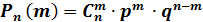
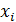
			…	m	…	N
			…		…

………………………………………………...

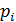
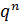
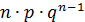
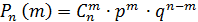
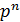
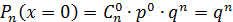
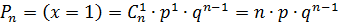
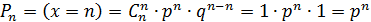
Теорема. Математическое ожидание дискретной случайной величины, распределенной по биномиальному закону, равняется произведению числа всех опытов на вероятность наступления события в отдельном опыте, то есть

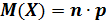
Дисперсия равняется произведению числа всех опытов на вероятность наступления и не наступления события в отдельном опыте, то есть

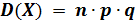
Пример.

По статистическим данным известно, что вероятность рождения мальчика p = 0,515.

Составить закон распределения числа мальчиков в семье с пятью детьми. Найти математическое ожидание 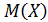, дисперсию 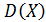, среднее квадратическое отклонение 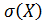, моду 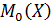, функцию распределения F(X) график.

Решение:

X ‒ случайная величина ‒ число мальчиков в семье с пятью детьми.

Составим закон распределения числа мальчиков в семье с пятью детьми:

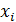
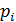
	0,026835	0,142475	0,302579	0,321296	0,170585	0,036227

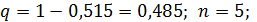
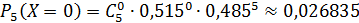
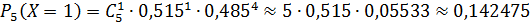
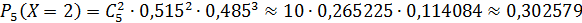
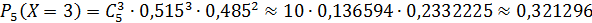
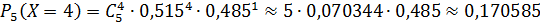
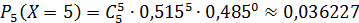
Проверка:

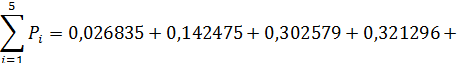
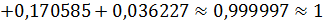
1. Математическое ожидание:

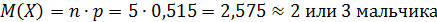
2. Дисперсия:

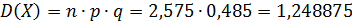
3. Средне квадратическое откланение:

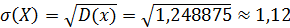
4. 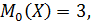так как при m = 3 вероятность максимальная, которая составляет p = 0,321296.