Лекция 8. НЕПРЕРЫВНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА, ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ, ПЛОТНОСТЬ ВЕРОЯТНОСТИ, ВЕРОЯТНОСТЬ ПОПАДАНИЯ В ЗАДАННЫЙ ИНТЕРВАЛ.
Непрерывной случайной величиной называют случайную величину, значения которой сплошь заполняют некоторый интервал.
Например, рост человека ‒ непрерывная случайная величина.
Функцией распределения случайной величины называют вероятность того, что случайная величина Х принимает значения, меньшие х.
F(x) = P(X 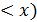
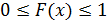
Геометрически формула F(x) = P(X 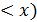 означает, что все значения Х будут находиться, левее х. Функция F(x) называется интегральной функцией.
означает, что все значения Х будут находиться, левее х. Функция F(x) называется интегральной функцией.
Пример.
Составить закон распределения числа библиотек, посещенных студентом в поисках нужной кни ъги, если число библиотек в городе равно 5. А вероятность наличия этой книги равна 0,3. При 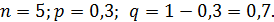 Найти функцию распределения.
Найти функцию распределения.
Решение:
Составим закон распределения:
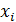
| |||||
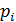
| 0,3 | 0,21 | 0,147 | 0,1029 | 0,2401 |
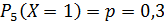
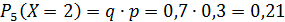
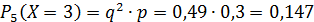
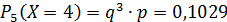
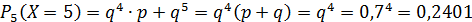
Проверка:
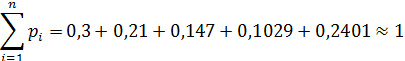
Найдем функцию распределения:
1. Если 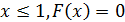
2. Если 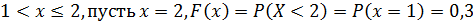
3. Если 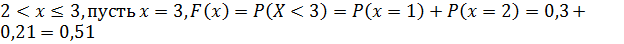
4. Если 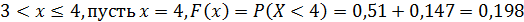
5. Если 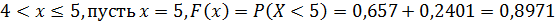
6. Если 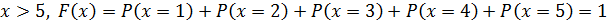
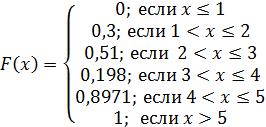
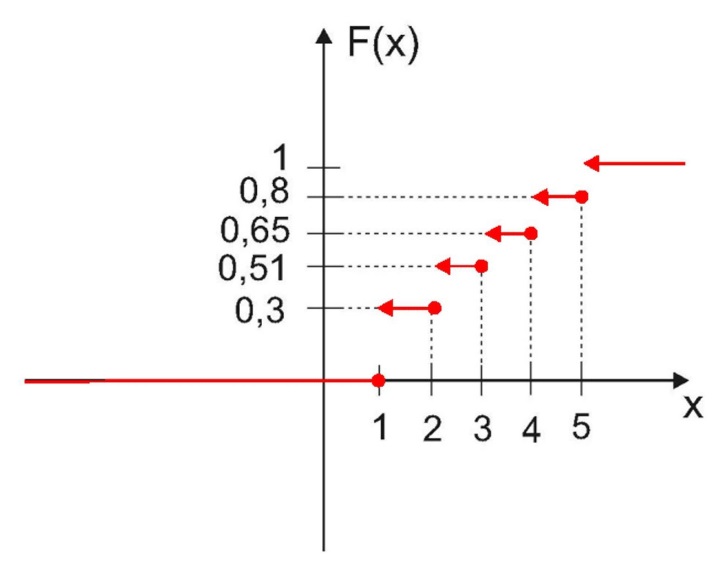
Плотностью вероятности непрерывной случайной величины f (x) называется производная от функции распределения этой случайной величины.
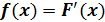
Следовательно, F(x) первообразная для f (x).
Теорема. Вероятность попадания непрерывной случайной величины X в интервал от a до b находится по формуле:
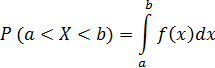
Доказательство.
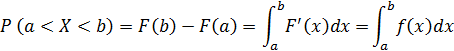
Следствие. Если все возможные значения случайной величины
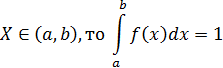
Дата добавления: 2015-12-16; просмотров: 1705;
