Равномерный закон распределения.
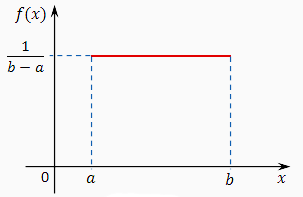
Непрерывная случайная величина Х имеет равномерный закон распределения (закон постоянной плотности) на отрезке [a; b], если на этом отрезке функция плотности вероятности случайной величины постоянна, то есть f (x) имеет вид:
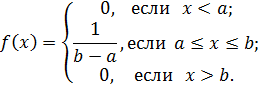
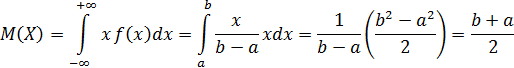
Следовательно, математическое ожидание случайной величины, равномерно распределенной на отрезке (a, b), равняется середине этого отрезка.
Дисперсия имеет вид:
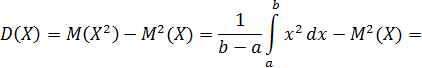
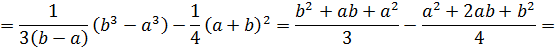
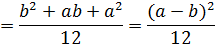
Найдем вероятность попадания значения случайной величины, имеющей равномерное распределение, на интервал 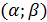 , принадлежащий целиком отрезку [a, b]:
, принадлежащий целиком отрезку [a, b]:
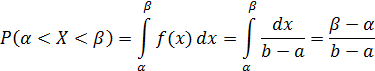
Следовательно,
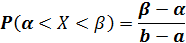
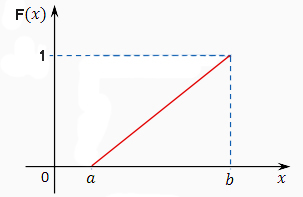
Функция распределения примет вид:
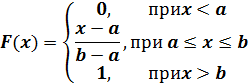
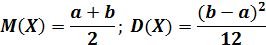
Пример.
Поезда метрополитена идут регулярно с интервалом 2 мин. Пассажир выходит на платформу в случайный момент времени. Какова вероятность того, что ждать пассажиру придется не больше полминуты.
Найти математическое ожидание и среднее квадратическое отклонение случайной величины X – времени ожидания поезда.
Решение:
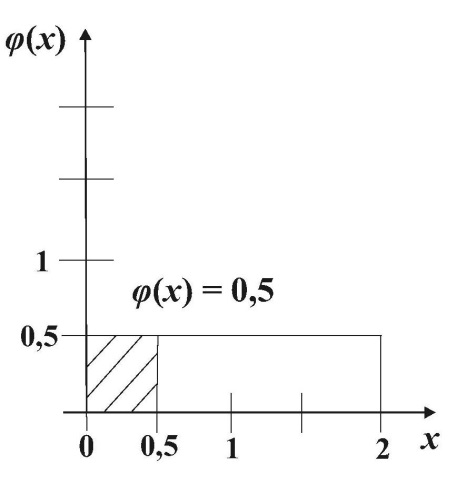
Случайная величина X – время ожидания поезда на временном (в минутах) отрезке [0;2] имеет равномерный закон распределения f(x)=1/2.
Поэтому вероятность того, что пассажиру придется ждать не более полминуты, равна 1/4 от равной единице площади прямоугольника, т.е.
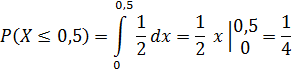
Найдем математическое ожидание, дисперсию и среднее квадратическое отклонение:
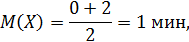
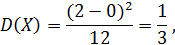
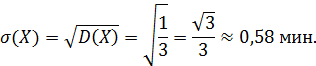
Дата добавления: 2015-12-16; просмотров: 4008;
