Распределение Пуассона дискретных случайных величин.
Дискретная случайная величина распределена по закону Пуассона, если она принимает значения 0,1,2…m…n…, бесконечное, но счетное число раз, с вероятностями, определяемыми по формуле Пуассона:
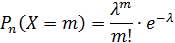
где 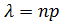 , p
, p 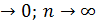 .
.
Закон распределения принимает вид:
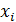
| … | m | … | |||
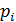
| 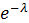
| 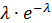
| 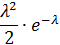
| … | 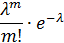
| … |
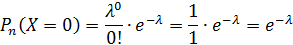
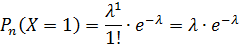
Теорема.Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, равны параметру Пуассона.
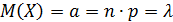
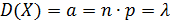
Пример 1.
Станок изготавливает за смену 100000 деталей. Вероятность изготовления бракованной детали p = 0,0001.
Найти вероятность того, что за смену будет изготовлено 5 бракованных деталей.
Решение:
Обозначим n = 100 000, k = 5, p = 0,0001. События, состоящие в том, что отдельная деталь бракована, независимы, число испытаний n велико, а вероятность p мала, поэтому воспользуемся распределением Пуассона:
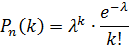
где 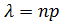
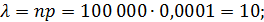
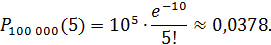
Пример 2.
Устройство состоит из 1000 элементов. Вероятность отказа любого элемента в течение времени t = 0,002.
Найти математическое ожидание 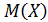 , дисперсию
, дисперсию 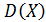 , среднеквадратическое отклонение
, среднеквадратическое отклонение 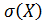 и моду
и моду 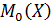 .
.
Решение:
X ‒ случайная величина ‒ число отказавших за время tэлементов.
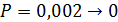
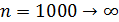
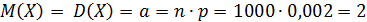 элемента
элемента
Составим закон распределения:
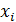
| … | m | … | ||||
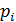
| 0,135335 | 0,270671 | 0,270671 | 0,180447 | … | 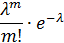
| … |
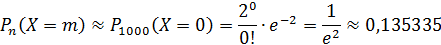
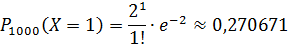
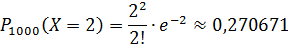
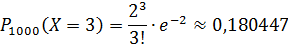
Дата добавления: 2015-12-16; просмотров: 2914;
