Анализ и синтез линейных стохастических систем при стационарных случайных воздействиях
1. Оценка динамической точности САУ по величине среднеквадратической ошибки. Спектральная плотность сигнала ошибки системы
Так как при действии случайных воздействий САУ постоянно находится в переходном процессе, то традиционная оценка качества при детерминированных воздействиях по величине перерегулирования s%, времени регулирования Тр, колебательности, установившейся ошибки eуст и т.д. является неоправданной. Теряет смысл оценка качества САУ и по мгновенным значениям сигнала ошибки, так как случайные процессы задаются характеристиками (законы распределения, математические ожидания, дисперсии, корреляционные функции, спектральные плотности), которые определяют их в среднем, по вероятности.
В этих условиях удобнее оценивать качество системы по величине ошибки в динамическом режиме. В качестве критерия, определяющего точность работы системы, обычно на практике принимают среднеквадратическое значение ошибки e(t), то есть квадратный корень из среднего значения квадрата ошибки
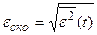 . (28.1)
. (28.1)
Для эргодических стационарных случайных процессов (28.1) можно записать
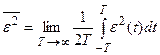 . (28.2)
. (28.2)
Этот критерий применяют в тех случаях, когда нежелательность ошибки возрастает. Так как корреляционная функция сигнала ошибки определяется
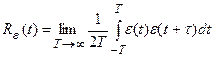 , (28.3)
, (28.3)
то из сравнения уравнений (28.2) и (28.3) следует, что среднее значение квадрата ошибки равно корреляционной функции ошибки при условии, когда t=0 (рис.28.1), то есть
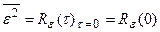 .
.
 |
Рис.28.1. Корреляционная функция сигнала ошибки
Известно, что
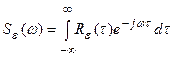 ,
,
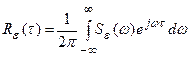 .
.
Следовательно, для момента, когда t=0
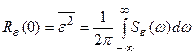 . (28.4)
. (28.4)
Учитывая, что спектральная плотность является четной функцией, уравнение (28.4) примет вид
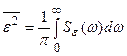 . (28.5)
. (28.5)
Полученная зависимость (28.5) является исходной для вычисления среднеквадратической ошибки (28.1).
Этот критерий применяют в тех случаях, когда нежелательность ошибки возрастает с ее величиной. При этом считают, что чем меньше величина среднеквадратической ошибки, тем точнее работает система. Такой критерий точности нашел широкое применение, но не является универсальным.
Чтобы оценить точность работы САУ при случайных воздействиях (28.5), необходимо знать значение спектральной плотности сигнала ошибки. Определим спектральную плотность сигнала ошибки линейной устойчивой САУ, структурная схема которой изображена на рис.28.2.
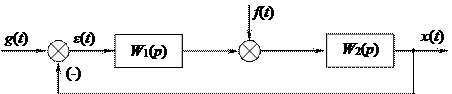 |
Рис.28.2. Структурная схема САУ
Полагаем, что параметры передаточных функций звеньев системы заданы, задающее g(t) и возмущающее f(t) воздействия являются независимыми, случайными стационарными сигналами с известными спектральными плотностями Sg(w) и Sf(w) и равными нулю средними значениями.
Из рис.28.2 следует, что значение сигнала ошибки определяется
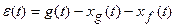 , (28.6)
, (28.6)
где 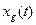 - составляющая выходного сигнала от g(t);
- составляющая выходного сигнала от g(t);
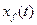 - составляющая выходного сигнала от f(t).
- составляющая выходного сигнала от f(t).
Уравнение (28.6) справедливо только для линейных систем и может быть записано в следующем виде:
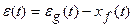 , (28.7)
, (28.7)
где
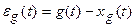 .
.
Запишем выражение для корреляционной функции сигнала ошибки САУ с учетом (28.7):
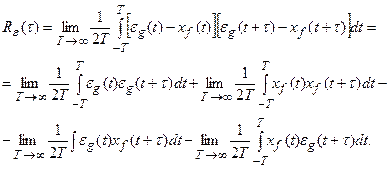 (28.8)
(28.8)
Из уравнения (28.8) следует:
- первое слагаемое является корреляционной функцией сигнала ошибки от задающего воздействия, т.е.
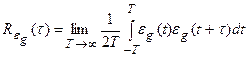 , (28.9)
, (28.9)
- второе слагаемое является корреляционной функцией выходного сигнала от возмущения, т.е.
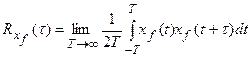 , (28.10)
, (28.10)
- третье и четвертое слагаемые равны нулю, так как являются взаимными корреляционными функциями сигналов eg и xf, а сигналы g и f – независимы.
Следовательно, уравнение (28.8) и учетом (28.9) и (28.10) примет вид:
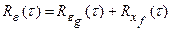 . (28.11)
. (28.11)
Взяв преобразование Фурье от (28.11), получим зависимость между спектральными плотностями:
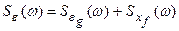 , (28.12)
, (28.12)
где
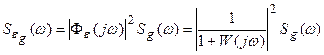 ,
,
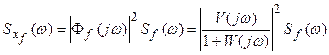 .
.
Следовательно, уравнение (12.12) можно записать
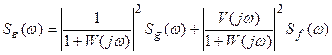 . (28.13)
. (28.13)
Для заданной САУ (рис.28.2) передаточные функции разомкнутых систем определяются как 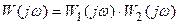 , а
, а 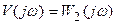 .
.
В том случае, когда возмущение приложено ко входу системы, уравнение (28.13) примет вид
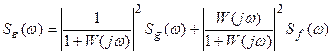 . (28.14)
. (28.14)
С помощью полученных выражений (28.13) и (28.14) можно определить спектральную плотность ошибки Se(w) по заданным спектральным плотностям Sg(w) и Sf(w) входных сигналов и амплитудно-фазовым характеристикам разомкнутой САУ, а следовательно, и среднеквадратическую ошибку (28.5). Ошибка системы на основании сделанных ранее предложений является стационарной функцией с равным нулю средним значением.
2. Понятие и вычисление среднеквадратической ошибки САУ аналитическим и графическим способами
На основании (28.4) выражение для определения среднего значения квадрата ошибки может быть записано следующим образом:
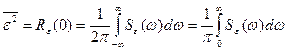 ,
,
где Se(w) – четная функция от w.
Очевидно, в случае действия независимых стационарных сигналов g(t), f(t), приложенных в разных точках системы, будем иметь
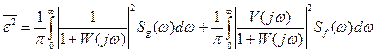 . (28.15)
. (28.15)
Если сигналы g(t) и f(t) приложены ко входу системы, то (28.15) примет вид
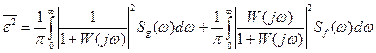 . (28.16)
. (28.16)
Таким образом, определение 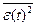 связано с вычислением интеграла (28.5).
связано с вычислением интеграла (28.5).
Этот интеграл может быть вычислен аналитически с использованием табличных интегралов или методом графоаналитического интегрирования.
Рассмотрим аналитический метод определения среднеквадратической ошибки системы.
Подынтегральные выражения каждого члена правой части уравнений (28.15) и (28.16) могут быть приведены к виду
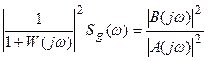 , (28.17)
, (28.17)
поскольку Sg(w) является четной функцией от w. Действительно, пусть
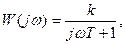
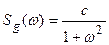 ,
,
тогда
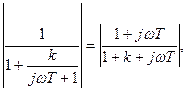
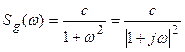 .
.
Таким образом,
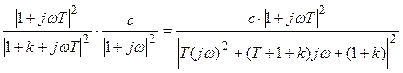 .
.
Так как 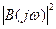 четная функция w, то в числителе (28.17) подынтегрального выражения нечетные степени w не надо учитывать, а необходимо учитывать лишь члены с четными степенями w, которые образуют некоторый многочлен
четная функция w, то в числителе (28.17) подынтегрального выражения нечетные степени w не надо учитывать, а необходимо учитывать лишь члены с четными степенями w, которые образуют некоторый многочлен 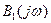 . Тогда
. Тогда
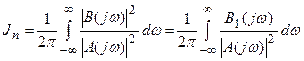 , (28.18)
, (28.18)
где
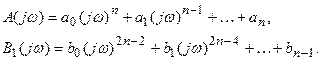
Этот интеграл может быть вычислен в явном виде для любого “n”. Такие вычисления произведены и их результаты приведены в виде таблиц в ряде работ через коэффициенты уравнений.
Например:
при n=1
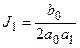 ;
;
при n=2
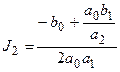 ;
;
при n=3
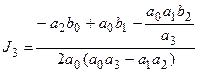 ;
;
и так далее.
 |
В нашем примере имеем:
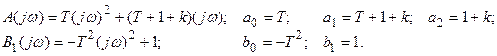
Следовательно,
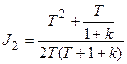 .
.
Для систем автоматического управления при n>4 аналитический метод определения среднего значения квадрата ошибки становится громоздким. Поэтому прибегают к графическому решению задачи. Для этого строится график спектральной плотности сигнала ошибки Se(w) и определяется площадь под построенной кривой. Точность решения задачи зависит от точности построения кривой Se(w) и определения ее площади (рис.28.3).
3. Синтез систем при случайных воздействиях [2]
Рассмотрим систему автоматического управления с передаточной функцией 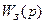 , служащую для усиления и преобразования управляющего полезного сигнала
, служащую для усиления и преобразования управляющего полезного сигнала 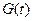 при наличии случайной помехи
при наличии случайной помехи 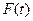 . Это преобразование в общем случае производится в соответствии с некоторым заданным оператором (алгоритмом преобразования)
. Это преобразование в общем случае производится в соответствии с некоторым заданным оператором (алгоритмом преобразования) 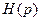 (рис. 28.4).
(рис. 28.4).
В общем случае система должна возможно более точно воспроизводить на своем выходе не само управляющее воздействие 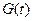 , а некоторую функцию от управляющего воздействия
, а некоторую функцию от управляющего воздействия
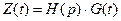 . (28.19)
. (28.19)
В системах, находящихся под воздействием случайного (или регулярного) полезного сигнала и случайной помехи, возникает задача отделения полезного сигнала от помехи и подавления (фильтрации) последней. Эту задачу называют задачей фильтрации или сглаживания.
Введение преобразующего оператора 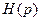 обобщает задачу не только на обычные следящие системы, у которых
обобщает задачу не только на обычные следящие системы, у которых 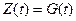 (т.е.
(т.е. 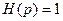 ), но и на другие классы систем, выполняющие различные преобразования управляющего сигнала.
), но и на другие классы систем, выполняющие различные преобразования управляющего сигнала.
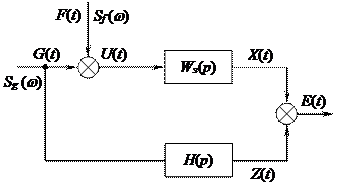 |
Рис. 28.4
В зависимости от вида оператора 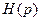 задача фильтрации сочетается с задачей воспроизведения (если
задача фильтрации сочетается с задачей воспроизведения (если 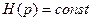 ), упреждения (предсказания), или экстраполяции (если
), упреждения (предсказания), или экстраполяции (если 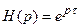 ), интегрирования (если
), интегрирования (если 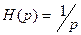 ), дифференцирования (если
), дифференцирования (если 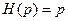 ) и др. В общем случае преобразующий оператор
) и др. В общем случае преобразующий оператор 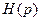 может быть произвольным. Идеальное преобразование полезного сигнала в соответствии с (28.19) невозможно из-за динамических ошибок системы, а также из-за наличия возмущающих воздействий (помех). Поэтому выходной сигнал (регулируемая величина)
может быть произвольным. Идеальное преобразование полезного сигнала в соответствии с (28.19) невозможно из-за динамических ошибок системы, а также из-за наличия возмущающих воздействий (помех). Поэтому выходной сигнал (регулируемая величина) 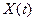 будет отличаться от воспроизводимого сигнала
будет отличаться от воспроизводимого сигнала 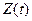 . Разность
. Разность
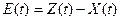 (28.20)
(28.20)
называют случайной ошибкой системы.
Синтез систем при случайных воздействиях заключается в определении динамических характеристик системы, наилучшим образом обеспечивающих выполнение некоторого статистического критерия оптимальности. Существуют различные статистические критерии оптимальности. Однако наиболее часто за статистический критерий оптимальности принимают критерий минимума средней квадратической ошибки:
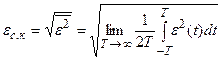 , (28.21)
, (28.21)
где 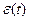 - любая реализация случайной ошибки.
- любая реализация случайной ошибки.
В этом случае задача синтеза состоит в том, чтобы найти такую физически реализуемую оптимальную передаточную функцию замкнутой системы 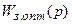 , при которой было бы минимальным среднее значение квадрата ошибки:
, при которой было бы минимальным среднее значение квадрата ошибки:
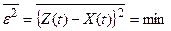 . (28.22)
. (28.22)
Согласно критерию средней квадратической ошибки оценка точности системы производится в зависимости от среднего, а не мгновенного значения ошибки, что не всегда является достаточным, например тогда, когда требуется, чтобы ошибка не выходила за заданные пределы. Применение этого критерия может оказаться нерациональным и в тех случаях, когда требования к величине ошибки в разные моменты времени неодинаковы.
Однако несмотря на то, что этот критерий, впрочем, как и всякий другой косвенный критерий, не является универсальным, он благодаря своей простоте получил широкое практическое применение.
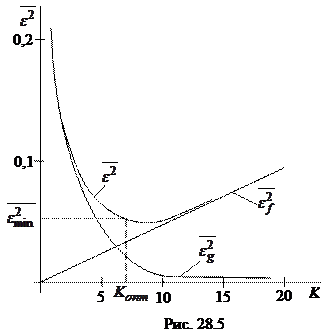 При воздействии на систему не коррелированных между собой стационарного сигнала и помехи среднее значение квадрата ошибки состоит из двух составляющих:
При воздействии на систему не коррелированных между собой стационарного сигнала и помехи среднее значение квадрата ошибки состоит из двух составляющих:
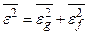
Если бы к системе было приложено только одно внешнее воздействие, либо полезный сигнал 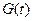 , либо помеха
, либо помеха 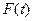 , то теоретически соответствующим выбором параметров передаточной функции (полосы пропускания) системы можно было бы обеспечить любую точность систем. Однако при одновременном действии полезного сигнала и помехи точность системы не может быть любой.
, то теоретически соответствующим выбором параметров передаточной функции (полосы пропускания) системы можно было бы обеспечить любую точность систем. Однако при одновременном действии полезного сигнала и помехи точность системы не может быть любой.
Это наглядно видно из рис.28.5, где изображены типичные графики зависимос-
ти составляющих ошибки 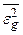 и
и 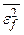 от значения коэффициента усиления разомкнутой системы K. Для лучшего воспроизведения управляющего сигнала
от значения коэффициента усиления разомкнутой системы K. Для лучшего воспроизведения управляющего сигнала 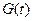 , т.е. уменьшения составляющей ошибки
, т.е. уменьшения составляющей ошибки 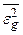 , система должна иметь возможно больший коэффициент усиления. Однако для того чтобы лучше подавлять помеху
, система должна иметь возможно больший коэффициент усиления. Однако для того чтобы лучше подавлять помеху 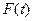 , т.е. уменьшить составляющую ошибки
, т.е. уменьшить составляющую ошибки 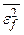 , система, наоборот, должна иметь возможно меньший коэффициент K. Поэтому, когда на систему действуют одновременно полезный сигнал и помеха, существуют некоторое комплексное (оптимальное) решение и соответствующие ему оптимальные параметры системы (в данном случае
, система, наоборот, должна иметь возможно меньший коэффициент K. Поэтому, когда на систему действуют одновременно полезный сигнал и помеха, существуют некоторое комплексное (оптимальное) решение и соответствующие ему оптимальные параметры системы (в данном случае 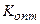 ), при которых среднее значение квадрата ошибки будет минимальным, меньше которого его, при заданных статистических характеристиках управляющего сигнала и помехи, никаким изменением параметров сделать нельзя.
), при которых среднее значение квадрата ошибки будет минимальным, меньше которого его, при заданных статистических характеристиках управляющего сигнала и помехи, никаким изменением параметров сделать нельзя.
В зависимости от вида графиков спектральной плотности управляющего сигнала и помехи способы решения задачи синтеза при случайных воздействиях могут быть различны.
В простейшем случае, когда спектры частот полезного сигнала 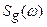 и помехи
и помехи 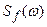 не налагаются друг на друга (рис. 28.6,а), амплитудно-частотную характеристику замкнутой системы
не налагаются друг на друга (рис. 28.6,а), амплитудно-частотную характеристику замкнутой системы 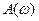 выбирают достаточно широкой для обеспечения требуемой точности воспроизведения управляющего сигнала и в то же время достаточно узкой для того, чтобы система меньше реагировала на помеху.
выбирают достаточно широкой для обеспечения требуемой точности воспроизведения управляющего сигнала и в то же время достаточно узкой для того, чтобы система меньше реагировала на помеху.
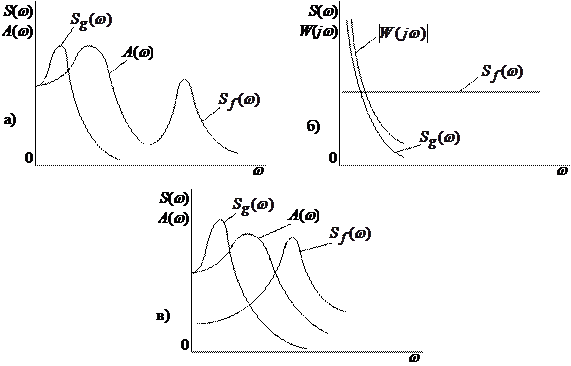 Если управляющий сигнал имеет спектр частот, очень быстро убывающий с возрастанием частоты, а спектр помех близок к белому шуму (рис.28.6,б), то в этом случае форма амплитудно-частотной характеристики
Если управляющий сигнал имеет спектр частот, очень быстро убывающий с возрастанием частоты, а спектр помех близок к белому шуму (рис.28.6,б), то в этом случае форма амплитудно-частотной характеристики  разомкнутой системы должна выбираться при низких частотах, где
разомкнутой системы должна выбираться при низких частотах, где  и сконцентрирована основная энергия управляющего сигнала, возможно более близкой к форме спектральной плотности управляющего сигнала
и сконцентрирована основная энергия управляющего сигнала, возможно более близкой к форме спектральной плотности управляющего сигнала 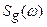 , а затем должна быстро убывать, по возможности следуя за убывающей характеристикой
, а затем должна быстро убывать, по возможности следуя за убывающей характеристикой 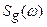 . В общем случае, когда спектры частот полезного сигнала и помехи накладываются друг на друга и имеют произвольную форму (рис. 28.6,в), определение оптимальных параметров системы становится довольно сложным.
. В общем случае, когда спектры частот полезного сигнала и помехи накладываются друг на друга и имеют произвольную форму (рис. 28.6,в), определение оптимальных параметров системы становится довольно сложным.
Рис. 28.6
При синтезе систем со случайными воздействиями различают два вида задач:
1. Синтез при заданной структуре системы управления, когда добиваются минимума средней квадратической ошибки, выбирая оптимальные параметры корректирующих звеньев системы на основании известных статистических характеристик полезного сигнала и помехи.
2. Синтез при произвольной структуре системы управления, когда по заданным статистическим характеристикам полезного сигнала и помехи определяют оптимальную структуру и параметры системы, при которых обеспечивается минимум средней квадратической ошибки.
Синтез при заданной структуре системы. В этом случае задача синтеза формулируется следующим образом. Заданы статистические характеристики полезного сигнала и помехи, например спектральные плотности 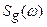 и
и 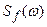 ; структура системы и ее передаточная функция
; структура системы и ее передаточная функция 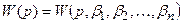 , где
, где 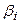 - параметры системы.
- параметры системы.
Требуется найти оптимальные параметры системы 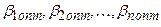 , при которых обеспечивается минимум средней квадратической ошибки.
, при которых обеспечивается минимум средней квадратической ошибки.
Эта задача решается следующим образом: зная спектральные плотности 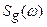 и
и 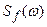 и передаточную функцию системы, определяют спектральную плотность ошибки
и передаточную функцию системы, определяют спектральную плотность ошибки 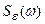 , а затем, пользуясь табличными интегралами, находят аналитическое выражение среднего значения квадрата ошибки
, а затем, пользуясь табличными интегралами, находят аналитическое выражение среднего значения квадрата ошибки 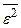 , которое получается зависящим от параметров системы:
, которое получается зависящим от параметров системы:
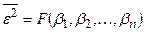 . (28.23)
. (28.23)
Дифференцируя (12.23) по 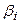 , где
, где 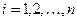 , и приравнивая нулю частотные производные, находят n уравнений, из которых определяют оптимальные параметры системы
, и приравнивая нулю частотные производные, находят n уравнений, из которых определяют оптимальные параметры системы 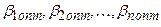 , обеспечивающие минимум средней квадратической ошибки.
, обеспечивающие минимум средней квадратической ошибки.
Как правило, большинство параметров системы изменять трудно либо невозможно, так как они определяются заданными техническими или конструктивными соображениями. Поэтому обычно выбирают два-три параметра, например постоянные времени корректирующих звеньев, коэффициент усиления разомкнутой системы и др. Если число переменных n невелико, то отыскание экстремума функции не вызывает затруднений. При большем числе n, когда явное выражение среднего значения квадрата ошибки через параметры системы определить затруднительно либо оно слишком громоздко, используют приближенные методы отыскания минимума выражения (28.23) путем числового задания интересующих параметров и построения соответствующих графиков.
Параметры системы, выбранные по критерию минимума средней квадратической ошибки, оценивают затем, исходя из возможности их технической реализации и допустимых динамических показателей системы (времени регулирования, наличия и величины перерегулирования и т.д.).
| <== предыдущая лекция | | | следующая лекция ==> |
| Прохождение случайного сигнала через линейные звенья | | | Задачи оптимального управления и критерии оптимальности |
Дата добавления: 2015-12-11; просмотров: 3167;
