Прохождение случайного сигнала через линейные звенья

1 Связь между корреляционными функциями выходного и входного сигналов

Рассмотрим линейную динамическую систему (рис.27.1), имеющую комплексную передаточную функцию Ф(jw) и импульсную переходную функцию w(t).

Рис.27.1. Структурная схема замкнутой линейной САУ

Требуется определить корреляционную функцию R_x(t) и спектральную плотность S_x(w) выходного сигнала x(t) рассматриваемой системы автоматического управления.

На основании интегральной связи между выходными и входными сигналами линейной стационарной системы имеем

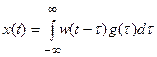. (27.1)

Вводя в это уравнение новую переменную 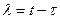, будем иметь

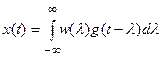. (27.2)

По аналогии можно получить и выражение для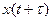

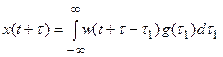. (27.3)

При введении новой переменной 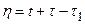уравнение (11.4) примет вид

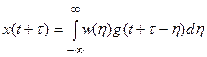. (27.4)

Так как выходной сигнал системы является стационарным случайным с равным нулю средним значением, то корреляционная функция выходного сигнала будет равна

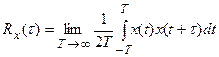. (27.5)

Подставив выражения (27.2) и (27.4) в формулу (27.5), получим

.

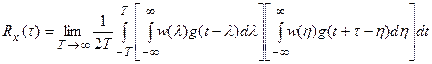Меняя порядок интегрирования, будем иметь:

.

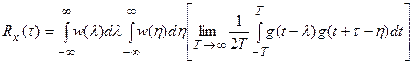Но для стационарного случайного процесса

.

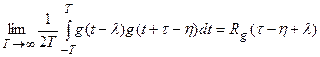Поэтому искомая корреляционная функция для выходного сигнала системы управления будет равна

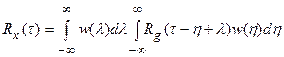. (27.6)

Таким образом, выражение (27.6) определяет искомое соотношение между корреляционными функциями входного g(t) и выходного x(t) сигналов исследуемой САУ.

2. Связь между спектральными плотностями случайных сигналов на входе и выходе линейной системы

Определим связь между спектральными плотностями выходного и входного сигналов.

Из уравнения спектральной плотности случайного процесса следует, что

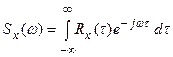. (27.7)

Подставляя в (27.7) выражение (27.6), запишем

.

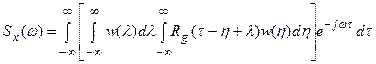Преобразуя это выражение и меняя порядок интегрирования, получим

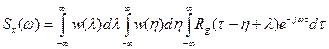. (27.8)

Вполне очевидно равенство

.

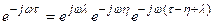Используя это равенство, выражение (27.8) примет вид

.

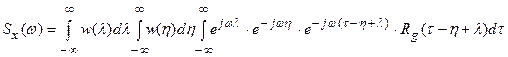Преобразуя это выражение и меняя порядок интегрирования, получим

.

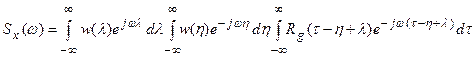Так как комплексная передаточная функция системы Ф(jw) и импульсная переходная функция w(t) являются преобразованиями Фурье друг от друга, то есть

,

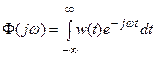то

,

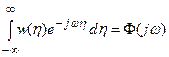а

.

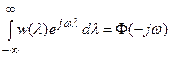Тогда выражение для спектральной плотности примет вид:

.

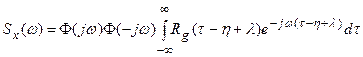Но

,

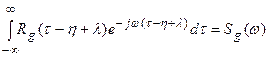а

.

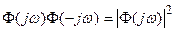Тогда выражение для спектральной плотности выходного сигнала примет такой вид:

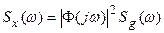. (27.9)

Полученное выражение устанавливает связь между спектральной плотностью выходного сигнала САУ и спектральной плотностью входного воздействия через квадрат модуля комплексной передаточной функции замкнутой системы.

Аналогична методика определения спектральной плотности выходного сигнала системы и для случая, когда к системе приложено как задающее воздействие g(t), так и возмущающее воздействие f(t), являющееся стационарными случайными функциями с равными нулю средними значениями. В случае, если между этими воздействиями взаимная корреляционная функция отсутствует, выражение для спектральной плотности выходного сигнала системы имеет вид

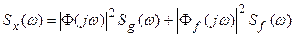, (27.10)

где 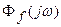- комплексная передаточная функция замкнутой системы по возмущающему воздействию;

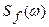- спектральная плотность входного возмущающего воздействия.

В частном, но часто встречающемся случае, когда точки приложения обоих воздействий g(t) и f(t) совпадают, т.е. 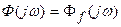, выражение примет вид

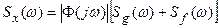. (27.11)

Для более общего случая, когда между задающим и возмущающим воздействиями существует взаимная корреляция, методика вывода выражения для спектральной плотности выходного сигнала системы аналогична ранее рассмотренной.