Задачи оптимального управления и критерии оптимальности
Общая характеристика оптимального управления
Задачи оптимального управления и критерии оптимальности
Теория оптимальных систем направлена на дальнейшее развитие и совершенствование систем автоматического управления. Основоположники – Л.С. Понтрягин, В.Г. Болтянский, А.А. Фельтбаум, А.М. Летов, американцы – Р. Беллман, Дж. Лейтман.
Два основных направления: теория детерминированных оптимальных систем (полная информация об объекте управления и приложенных воздействиях) и теория оптимального управления при случайных воздействиях (информация носит случайный характер).
Задача определения оптимального управления для линейных объектов, описываемых линейными дифференциальными уравнениями, в значительной степени решена. Для нелинейных объектов продолжается разработка теории.
Различают две формы оптимального управления:
- разомкнутая форма оптимального управления как функция времени (оптимальная программа);
- замкнутая форма оптимального управления как функция переменных состояния (оптимальный регулятор).
САУ называют оптимальной, если она является наилучшей в каком-либо смысле.
Наилучшие свойства системы определяются критериями качества, которые отражают различные стороны качества этой системы: точность, быстродействие, экономичность, надежность, сложность построения системы (ее структуру).
Основная задача управления динамическим объектом заключается в переводе объекта управления из некоторого начального состояния x(t0) в произвольно заданное конечное состояние x(tк) (x(t) – вектор состояния системы; t0, tк – начальный и конечный моменты времени управления).
Граничные или краевые условия – это совокупность начального и конечного состояний системы x(t0), x(tк).
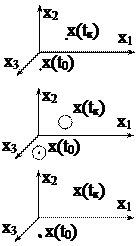Краевые условия могут иметь различный характер.
а) Краевые условия с закрепленными (фиксированными) концами, когда x(t0), x(tк) определяются соответствующими точками, фиксированными в пространстве состояния системы.
б) Краевые условия с подвижными концами (или одним подвижным концом) в этом случае векторы состояния x(t0), x(tк) или один из них ограничены некоторыми областями (линия, поверхность, гиперповерхность).
в) Краевые условия со свободным концом, здесь на вектор состояния x(tк) никаких условий не накладывается.
Дата добавления: 2015-12-11; просмотров: 994;