Классификация задач оптимального управления
А. По виду ограничений различают задачи оптимального управления
а) классического типа, когда ограничения задаются в виде равенства
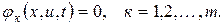
б) неклассического типа, когда ограничения задаются в виде неравенств
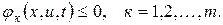
Б. По виду краевых условий различают задачи
а) с фиксированными (закрепленными) концами x(t0), x(tк) – точки в пространстве состояния.
б) с подвижным правым концом ( x(tк) состоит из более, чем одной точки), с подвижным левым концом ( x(t0) состоит из более, чем одной точки), с подвижными концами.
в) со свободным правым концом (на x(tк) никаких ограничений не накладывается).
В. По времени начала и окончания оптимального процесса различают задачи
а) с фиксированным временем, когда начальный t0 и конечный tк моменты фиксированы (заданы).
б) с нефиксированным временем, когда один из моментов времени t0 или tк не фиксирован.
Г. По критерию оптимальности различают
а) задачу Больца, критерий оптимальности имеет вид
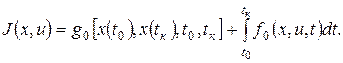
б) задачу Лагранжа, при этом критерий имеет вид
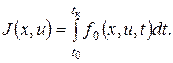
в) задачу Майера, при этом критерий имеет вид
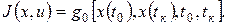
Задача Майера, в частном случае, когда функционал имеет вид 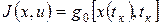 называется задачей терминального управления, когда
называется задачей терминального управления, когда 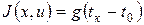 – задачей максимального (оптимального) быстродействия.
– задачей максимального (оптимального) быстродействия.
Задачи Больца, Лагранжа, Майера эквивалентны в том смысле, что путем преобразования переменных можно от одной задачи перейти к другой.
3. Классическое вариационное исчисление
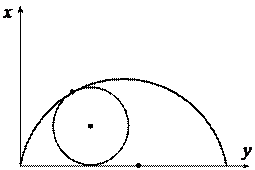
Иоган I Бернулли (швейцарец, 1667 г. – 1748 г.) в 1696 году поставил новую для математиков задачу: в вертикальной плоскости даны две траектории точки А и В. Требуется определить путь АМВ, опускаясь по которому под действием собственной тяжести, тело М, начав двигаться из точки А, дойдет до точки В в кратчайшее время.
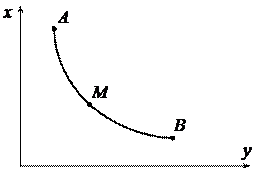 |
Решение задачи было получено И. Бернулли, а также Г. Лейбницем, Я. Бернули, Ньютоном.
Оказалось, что линией наискорейшего спуска (брахистохроной) является циклоида (это плоская кривая, которую описывает точка, закрепленная на окружности при ее качении без скольжения по неподвижной прямой).
 |
И. Бернулли поставил перед своим учеником Эйлером (тоже швейцарец) проблему найти общий путь решения таких задач.
В 1744 году Эйлер опубликовал работу, в которой новое направление в математике названо вариационным исчислением. Рассмотрим некоторые понятия вариационного исчисления.
Переменная величина J(x(t)) называется функционалом, зависящим от функции x(t), если каждой функции x(t) (из некоторого класса функций) соответствует число J. Аналогично определяют функционал от нескольких функций J[x(t), u(t)].
Вариационная задача с закрепленными концами
Рассмотрим простой функционал вида
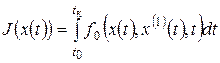 (29.1)
(29.1)
Этот функционал зависит только от параметров состояния x, x(1) и не зависит в явном виде от управления.
Пусть уравнения объекта управления имеют вид
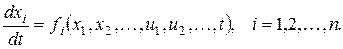
Концевые условия X(t0), X(tк).
Ограничения 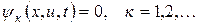 .
.
Уравнение Эйлера для нахождения функции x*(t), доставляющей экстремум функционалу (*) имеет вид
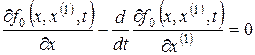
Представим уравнение Эйлера в развернутом виде.
Так как
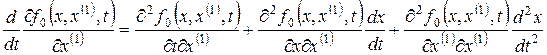 ,
,
то получим
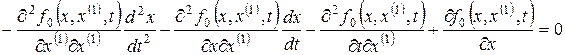
Решения этого уравнения x*(t, c1, c2), где c1, c2 – постоянные интегрирования, определяемые краевыми условиями
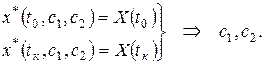
Рассмотрим пример: Требуется определить кривую x*(t), проходящую через концевые точки x(t0)=x0 и x(tк)=xк в моменты времени t0 и tк, на которой достигается экстремум функционала
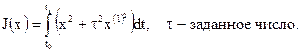
Имеем 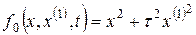 уравнение Эйлера имеет вид
уравнение Эйлера имеет вид 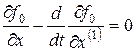
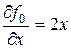 ;
; 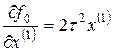
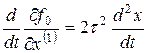 . В результате имеем
. В результате имеем 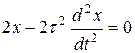 или
или 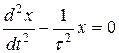 . Характеристическое уравнение
. Характеристическое уравнение 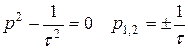 .
.
Решение 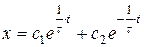 . Постоянные интегрирования находим из условия
. Постоянные интегрирования находим из условия
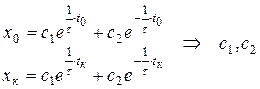
Дата добавления: 2015-12-11; просмотров: 2282;
