Критерии оптимальности

Перевод объекта управления из начального в конечное состояние для оптимальной системы должен выполняться с наилучшим качеством.

Критерий качества управления обычно задается в виде функционала

,

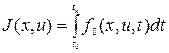где x – переменные состояния системы;

u – управляющие воздействия.

Функционал – это функция от функции. Функционал это некоторая числовая функция, определенная на некотором множестве функции.

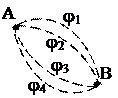
F(j) - время перевода материальной точки из положения А в положение В в зависимости от вида кривых (функция), соединяющих эти точки.

Численное значение функционала J(x,u) зависит от вида функции x(t), u(t).

Функционал J(x,u) называют показатель качества, критерий оптимальности, целевая функция.

Этот функционал качества выбирают таким образом, чтобы он выражал или величину выигрыша max J(x,u) (к.п.д., производительность) или величину потерь min J(x,u) (затраты времени, энергии).

Практически удобнее выбирать функционал качества J(x,u) таким образом, чтобы оптимальный процессу соответствовал его минимум (min J(x,u) ).

Для систем оптимальных по быстродействию, функционал качества имеет вид

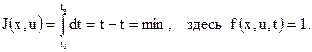
Для оптимизации систем по расходу топлива используется функционал вида

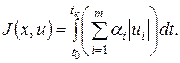
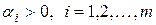– некоторые весовые коэффициенты, отражающие расход топлива на управление.

Для оптимизации систем с учетом времени переходного процесса и расхода топлива на управление

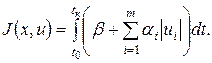
где b, a_i >0 – соответствующие весовые коэффициенты.

Ограничения

На переменные состояния объекта управления X(x₁, x₂, ¼, x_n) накладываются ограничения, которые определяются дифференциальными уравнениями объекта управления

.

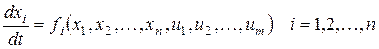Эти ограничения называют неголономными связями.

На переменные состояния x₁, x₂, ¼, x_n и управления могут накладываться ограничения вида

.

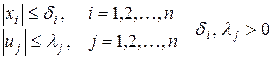Это объясняется ограничением на мощности приводов и прочностью конструкции ОУ и условиями нормальной эксплуатации.

Управления, удовлетворяющие условию ½u_j½£l_i,, называют допустимыми. Допустимые управления могут быть кусочно-непрерывными, кусочно-постоянными функциями. Именно такие управления обеспечивают оптимальные режимы.

Задача оптимального управления формулируется следующим образом:

- для заданных уравнений объекта управления

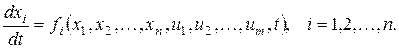
(или векторной форме ).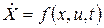

- ограничениях на управление и фазовые координаты вида , .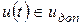

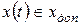- и краевых условиях X(t₀), X(t_к) (левый и правый концы траектории).

Требуется найти такие оптимальные управления u^*(t) и траекторию состояния x^*(t), при которых критерий качества J(x,u) принимает минимальное значение

.

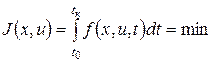Примеры постановки задач оптимального управления:

А. Вывод летательного аппарата (ЛА) в заданную точку пространства состояния за минимальное время.

Б. Перевод летательного аппарата на максимальную длительность.

В. Вывод летательного аппарата на максимальную высоту.

Г. Поворот вала двигателя на заданный угол за минимальное время.

Д. Поворот вала двигателя на заданный угол за время Т при минимальном расходе энергии.