Уравнения Эйлера-Лагранжа
Вариационные задачи на условный экстремум (связанный экстремум) появляются тогда, когда экстремум функционала отыскивается с учетом дополнительных условий, например, заданной системы дифференциальных уравнений объекта управления.
Пусть заданы дифференциальные уравнения объекта управления
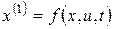 (а)
(а)
или
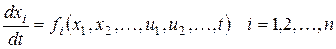
Требуется найти экстремали функционала
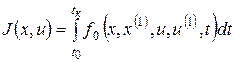 (б)
(б)
Краевые условия x(t0)=x0 , x(tк)=xк.
Вводится новый функционал
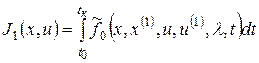 (в)
(в)
в котором
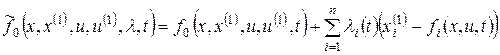
где l(t) – n-мерный вектор, элементами которого являются множители Лагранжа.
С помощью этих множителей Лагранжа задача об условном (а) экстремуме функционала (б) сводится к отысканию безусловного экстремума функционала (в).
Линейная часть приращения функционала по отношению к dx называется вариацией функционала и обозначается dJ. Вариация функционала аналогична дифференциалу функции dx.
Известно, что если некоторая функция в точке t0 имеет экстремум, то dx=0 (dJ=0).
Таким образом, чтобы функционал имел экстремум, его вариация dJ должна равняться нулю (dJ=0). Функции, на которых вариация функционала dJ=0, называются экстремалями.
Рассмотрим упрощенный вывод уравнения Эйлера. Пусть задан функционал
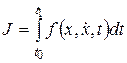 (1)
(1)
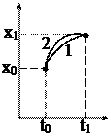 Требуется найти функцию, которая дает минимум функционалу (1). Требуется найти уравнение такой линии 1, которое при подстановке в функционал J давало бы ему экстремум.
Требуется найти функцию, которая дает минимум функционалу (1). Требуется найти уравнение такой линии 1, которое при подстановке в функционал J давало бы ему экстремум.
Предположим, что такая линия найдена, то есть найдена функция ее описывающая. Проварьируем эту функцию и определим приращение функционала (dJ – вариация функционала, dx – дифференциал функции).
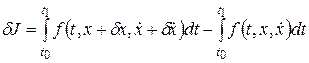 .
.
Вариацию аргумента выберем таким образом, чтобы dx(t0)=0 и dx(t1)=0, то есть варьируемая линия 2 должна проходить через точки x(t0), x(t1).
После разложения этого уравнения в ряд Тейлора и линеаризации, то есть учета только линейной части, получим
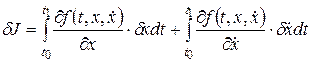
Интегрируя по частям второй член и преобразуя, найдем выражение
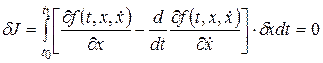 (2)
(2)
(для экстремали мы должны потребовать dJ=0)
По лемме Лагранжа интеграл (2) равен нулю только тогда, когда
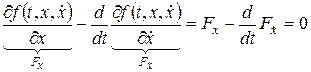 (3)
(3)
Уравнение (3) является уравнением Эйлера. Среди решений этого уравнения следует искать экстремали.
Рассмотрим уравнение Эйлера-Пуассона. Выражение для функционала качества имеет вид
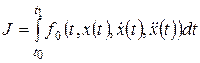 (*)
(*)
Функцию f0 считают дифференцируемой по своим аргументам необходимое число раз. Заданы граничные условия 
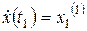 , где
, где 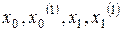 – заданные числа.
– заданные числа.
Решение уравнения
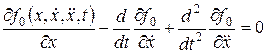
Дата добавления: 2015-12-11; просмотров: 1131;
