Анализ линейных дискретных СУ
1. Необходимые и достаточные условия устойчивости импульсных систем
Устойчивость является необходимым условием работоспособности любой системы. Под устойчивостью понимают способность системы возвращаться в положение равновесия после снятия воздействий, которые вывели систему из этого положения. Устойчивость дискретных систем, как и непрерывных, определяется по затуханию свободных колебаний переходного процесса с течением времени. Если свободные колебания переходного процесса обозначить через yсв(n), то дискретная система будет устойчивой при
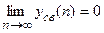
и неустойчивой, если
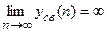 .
.
Система будет находиться на границе устойчивости при выполнении условия
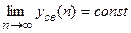 .
.
Известно, что свободное движение по заданному разностному уравнению дискретной системы определяется как общее решение соответствующего однородного уравнения:
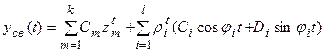 , (20.1)
, (20.1)
где zm (m=1,2,¼,k) – вещественные корни характеристического уравнения;
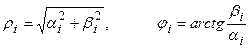 ,
,
где 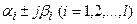 - комплексные корни характеристического уравнения;
- комплексные корни характеристического уравнения;
Cm, Cj, Dj – произвольные постоянные.
Как видно из (20.1), свободное движение со временем будет затухать до нуля, если модули всех корней характеристического уравнения дискретной системы будут меньше единицы:
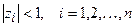 , (20.2)
, (20.2)
где n – порядок характеристического уравнения системы.
Полученная зависимость (20.2) и определяет необходимые и достаточные условия устойчивости дискретной системы по z-характеристическому уравнению этой системы.
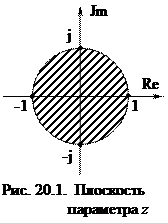 Если обратиться к плоскости z (рис.20.1), то указанные условия сводятся к тому, чтобы все корни z-характеристического уравнения системы лежали внутри окружности единичного радиуса.
Если обратиться к плоскости z (рис.20.1), то указанные условия сводятся к тому, чтобы все корни z-характеристического уравнения системы лежали внутри окружности единичного радиуса.
При переходе к билинейному преобразованию 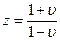 окружность единичного радиуса плоскости параметра z отображается на мнимую ось плоскости параметра u, а круг единичного радиуса плоскости параметра z отображается на левую полуплоскость плоскости параметра u. Это означает, что если z-характеристическое уравнение 1 + W(z) = 0 имеет все
окружность единичного радиуса плоскости параметра z отображается на мнимую ось плоскости параметра u, а круг единичного радиуса плоскости параметра z отображается на левую полуплоскость плоскости параметра u. Это означает, что если z-характеристическое уравнение 1 + W(z) = 0 имеет все
корни внутри окружности единичного радиуса, то полученное после билинейного преобразования характеристическое уравнение относительно параметра u
1 + W(u) = 0
будет иметь все корни в левой полуплоскости плоскости параметра u. Следовательно, необходимым и достаточным условием устойчивости дискретной системы по u-характеристическому уравнению является расположение всех корней этого уравнения в левой полуплоскости.
2. Аналог критерия устойчивости Гурвица
Критерий устойчивости Гурвица для непрерывных систем применялся к рациональным полиномам и выявлял факт наличия или отсутствия правых корней характеристического уравнения.
Z-характеристическое уравнение 1+W(z)=0 представляет собой рациональный полином относительно параметра z, но требование к устойчивости по этому уравнению не связано с наличием или отсутствием правых корней, поэтому критерий Гурвица в этом случае не может быть применим.
При переходе к билинейному преобразованию характеристическое уравнение 1+W(u)=0 по-прежнему остается рациональным полиномом, но факт устойчивости дискретной системы уже определяется наличием или отсутствием правых корней этого уравнения. Поэтому к u-характеристическому уравнению критерий устойчивости Гурвица может быть применен.
Таким образом, методика применения этого критерия сводится к следующему:
- к z-характеристическому уравнению исследуемой дискретной системы 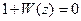 применяют билинейное преобразование
применяют билинейное преобразование 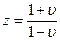 ;
;
- к полученному характеристическому уравнению относительного параметра u 1+W(u)=0 применяют критерий устойчивости Гурвица без каких-либо изменений, как и для непрерывных систем.
3. Аналог частотного критерия устойчивости Михайлова
Пусть характеристическое уравнение дискретных систем имеет вид
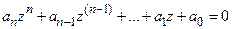 .
.
Тогда выражение для характеристического вектора D(z) можно представить следующим образом:
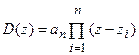 ,
,
где zi (i=1,2,...,n) – корни характеристического уравнения.
Для доказательства критерия Михайлова так же, как это было и для непрерывных систем, воспользуемся принципом аргумента. Определим приращение аргумента вектора D(z) при изменении z по окружности единичного радиуса против часовой стрелки на один оборот:

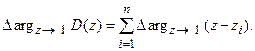
Найдем приращение аргумента вектора (z-zi) при изменении z по окружности единичного радиуса против часовой стрелки на один оборот для случаев, когда корень находится внутри (zi) и вне (zk) окружности единичного радиуса.
Очевидно (рис.20.2), для корня zi имеем
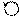
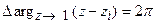 ,
,
а для корня zk (рис.20.3) получаем
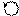
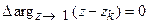 .
.
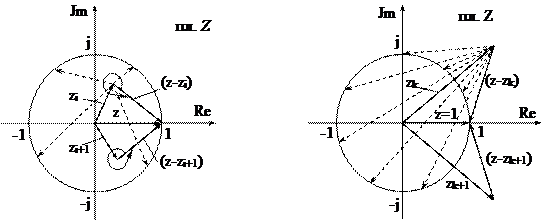 |
| Рис. 20.2. Приращение аргумента для корней внутри единичной окружности | Рис. 20.3. Приращение аргумента для корней вне единичной окружности |
Если все корни характеристического уравнения n-го порядка лежат внутри круга единичного радиуса, что соответствует устойчивой системе, то тогда должно выполняться следующее условие:

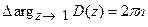 . (20.3)
. (20.3)
Если же среди n корней характеристического уравнения q корней будут лежать вне окружности единичного радиуса (система неустойчива), то тогда будем иметь
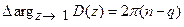 . (20.4)
. (20.4)
Поскольку вещественная часть характеристического вектора D(z) является четной функцией, то его годограф при изменении z по окружности единичного радиуса на один оборот будет кривой, симметричной относительно вещественной оси. Поэтому для анализа достаточно построить лишь одну ветвь, например, при изменении z по окружности единичного радиуса против часовой стрелки от точки +1 до –1, т.к. вторая ветвь будет зеркальным отображением первой.
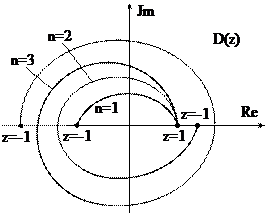
Рис. 20.4. Кривые Михайлова для устойчивых САУ
Очевидно, выражения (20.3) и (20.4) при этом будут иметь следующий вид:
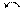
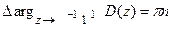 (20.5)
(20.5)
и

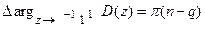 . (20.6)
. (20.6)
На основании (20.5) может быть сформулирован аналог критерия устойчивости Михайлова для дискретных систем. Дискретная система будет устойчивой, если при изменении z по окружности единичного радиуса против часовой стрелки на половину оборота от +1 до –1, характеристический вектор системы D(z) повернется в положительном направлении на угол pn, где n – порядок характеристического уравнения системы.
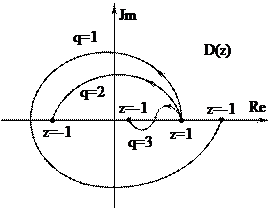
Рис. 20.5. Кривые Михайлова для неустойчивых САУ
На рис.20.4 показаны годографы характеристического вектора D(z) устойчивых систем первого, второго и третьего порядков (n=1,2,3). Годографы неустойчивой системы третьего порядка для различного числа корней характеристического уравнения, лежащих вне круга единичного радиуса (q=1,2,3), изображены на рис.20.5.
4. Аналог частотного критерия устойчивости Найквиста
Введем в рассмотрение некоторую функцию
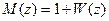 ,
,
где 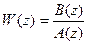 - передаточная функция разомкнутой системы.
- передаточная функция разомкнутой системы.
Далее получаем
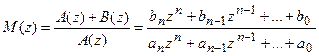 ,
,
где A(z) – характеристический полином разомкнутой системы;
A(z)+B(z) – характеристический полином замкнутой системы.
Выражение для M(z) можно представить так
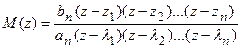 ,
,
где zi (i=1,2,...n) – корни характеристического уравнения замкнутой системы;
lj (j=1,2,...n) – корни характеристического уравнения разомкнутой системы.
Найдем приращение аргумента вектора M(z) при изменении z по окружности единичного радиуса против часовой стрелки на один оборот:

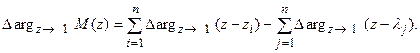
Для того, чтобы дискретная система была в замкнутом состоянии устойчивой, необходимо потребовать, чтобы все корни zi (i=1,2,¼,n) лежали внутри окружности единичного радиуса, а разомкнутая система при этом в общем случае может быть неустойчивой и иметь q корней характеристического уравнения, которые будут лежать вне окружности единичного радиуса.
В этом случае получаем
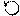
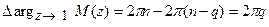 . (20.7)
. (20.7)
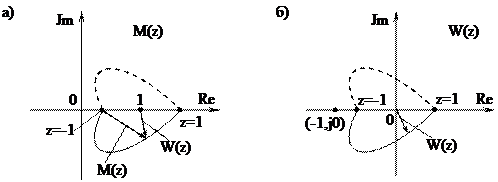 |
Рис. 20.6. Кривые M(z) и W(z)
На рис.20.6,а показан годограф вектора 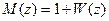 . Если ось ординат (рис.20.6,а) перенести на единицу вправо (рис.20.6,б), то тогда охват годографом вектора M(z) начала координат на рис.20.6,а будет соответствовать охвату годографом вектора W(z) (амплитудно-фазовая частотная характеристика разомкнутой системы) точки с координатами (-1,j0) на рис.20.6,б (эту точку называют критической). Это обстоятельство позволяет для оценки устойчивости дискретной системы в замкнутом состоянии вместо годографа M(z) строить амплитудно-фазовую характеристику разомкнутой системы W(z). Условие (20.7) позволяет сформулировать аналог критерия устойчивости Найквиста для дискретных систем.
. Если ось ординат (рис.20.6,а) перенести на единицу вправо (рис.20.6,б), то тогда охват годографом вектора M(z) начала координат на рис.20.6,а будет соответствовать охвату годографом вектора W(z) (амплитудно-фазовая частотная характеристика разомкнутой системы) точки с координатами (-1,j0) на рис.20.6,б (эту точку называют критической). Это обстоятельство позволяет для оценки устойчивости дискретной системы в замкнутом состоянии вместо годографа M(z) строить амплитудно-фазовую характеристику разомкнутой системы W(z). Условие (20.7) позволяет сформулировать аналог критерия устойчивости Найквиста для дискретных систем.
Дискретная система в замкнутом состоянии будет устойчивой, если при изменении переменной z по окружности единичного радиуса против часовой стрелки на один оборот амплитудно-фазовая характеристика разомкнутой системы W(z) будет охватывать критическую точку (-1,j0) в положительном направлении q раз, где q – число корней характеристического уравнения разомкнутой системы, лежащих вне круга единичного радиуса.
Поскольку АФХ W(z) является симметричной относительно вещественной оси, для исследования достаточно построить одну ветвь этой характеристики, например, при изменении переменной z по половине окружности единичного радиуса в положительном направлении от точки +1 до –1. Очевидно, в этом случае число охватов АФХ W(z) точки (-1,j0) уменьшится вдвое и будет равно 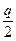 .
.
На рис.20.7 показаны различные варианты АФХ W(z) разомкнутых дискретных систем при q=1,2,3, которым соответствуют устойчивые в замкнутом состоянии системы.
Остановимся на особенностях использования аналога критерия устойчивости Найквиста для астатических систем. Дискретная система будет астатической, если z-передаточная функция разомкнутой системы содержит полюса, равные единице. Причем кратность таких полюсов определяет порядок астатизма системы. Например, z-передаточная функция астатической n-го порядка системы имеет вид
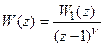 , (20.8)
, (20.8)
где 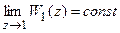 .
.
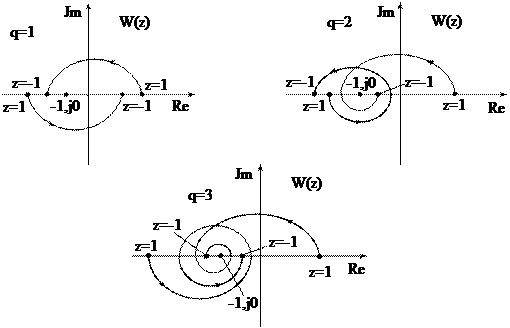 |
Рис. 20.7. Кривые Найквиста
Как видно, из (20.8), при построении АФХ разомкнутой системы для z=1 модуль W(z) обращается в бесконечность и возникает неопределенность в изображении амплитудно-фазовой характеристики. Для того, чтобы избежать этой неопределенности при построении АФХ W(z), точку z=1обходят по окружности бесконечно малого радиуса r против часовой стрелки (рис.20.8), то есть вместо z, только для этой точки в знаменатель выражения (20.8) подставляют
 .
.
 |
Рис. 20.8. Плоскость параметра Z
В результате получаем для n=1
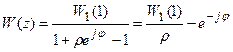 . (20.9)
. (20.9)
В этом случае корень z-характеристического уравнения разомкнутой системы, равный 1, как бы относят во внутрь окружности единичного радиуса. При этом АФХ разомкнутой системы на основании выражения (20.9) должна дополняться дугой бесконечно большого радиуса на угол от 0 до -p/2. Это при астатизме первого порядка, а в общем случае на угол от 0 до -p/2n.
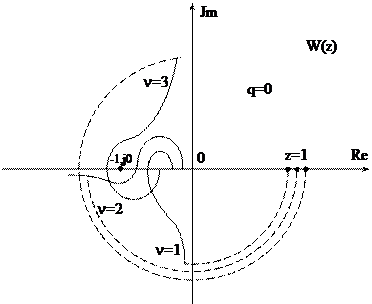 |
Рис. 20.9. Кривые Найквиста для астатических систем
После такого дополнения при построении АФХ разомкнутой астатической системы аналог критерия Найквиста применяется без каких-либо изменений.
На рис.20.9 показаны АФХ разомкнутых астатических систем (q=0, n=1,2,3), которым соответствуют устойчивые в замкнутом состоянии системы.
| <== предыдущая лекция | | | следующая лекция ==> |
| Примеры систем управления | | | Синтез дискретных систем |
Дата добавления: 2015-12-11; просмотров: 2600;
