Синтез дискретных систем
1. Построение переходного процесса дискретной СУ. Показатели качества
Качество процесса управления дискретных систем, так же как и непрерывных, прежде всего, определяется по кривой переходного процесса при различных типовых задающих и возмущающих воздействиях. В том случае, когда не располагают кривой переходного процесса, прибегают к различным косвенным оценкам качества управления.
Рассмотрим различные способы построения переходного процесса дискретной системы. Для построения кривой переходного процесса весьма широко используются разностные уравнения системы, которые представляют собой рекуррентные соотношения, позволяющие вычислять последующие значения искомой функции на основании информации о предыдущих значениях искомой функции и приложенных к системе возмущений.
Запишем разностные уравнения в виде:
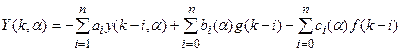 , (21.1)
, (21.1)
где y, g, f - соответственно выходная координата, задающее и возмущающее воздействия
системы.
Далее последовательно задаются значения k=0,1,2,¼ и на каждом этапе находятся выражения для 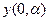 ,
, 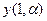 ,
, 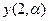 ,¼, то есть значения выходной координаты для интервалов времени
,¼, то есть значения выходной координаты для интервалов времени 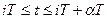 :
:
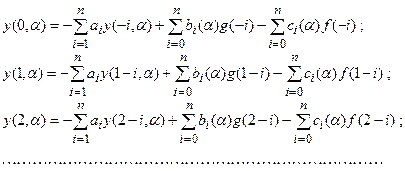 (21.2)
(21.2)
Если начальные условия нулевые, то есть система находилась в покое до момента приложения внешних воздействий, то тогда для k=0 имеем
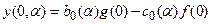
и далее в соответствии с (21.2).
Для определения процесса только в дискретные моменты времени полагают a=0. Если задано z-преобразование выходного сигнала системы, то наиболее простым способом получения оригинала является разложение этого z-преобразования в ряд Лорана.
При использовании формулы обращения искомая функция времени определяется сразу в виде аналитического выражения. Однако получение этого выражения нередко приводит к значительным трудностям.
При определении показателей качества дискретных систем, как и непрерывных, обычно используется переходная характеристика. Если ординаты этой характеристики получены только для дискретных моментов времени, то она легко может быть аппроксимирована с помощью плавной огибающей. Далее могут быть найдены такие показатели качества, как перерегулирование, время переходного процесса, колебательность, ошибка в установившемся режиме.
Переходная функция может быть построена с использованием обратного Z-преобразования при подаче на вход системы z–преобразованного единичного ступенчатого воздействия. Обратное z-преобразование позволяет по z-преобразованиюнекоторой функции F(z) найти ее оригинал. Если известно z-преобразование выходной величины, то можно определить соответствующую ему функцию времени, т.е. найти переходный процесс в системе. Необходимо иметь в виду, что обратное z-преобразование позволяет определить значения соответствующей функции времени только для моментов квантования.
По известному z-преобразованию соответствующую функцию времени можно найти следующими путями.
1. Посредством таблиц z-преобразования. В этом случае z-преобразование сложного вида разлагается на простые составляющие таким образом, чтобы обратное z-преобразование каждой составляющей могло быть определено из таблицы. Действительно, если 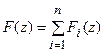 , причем обратное z-преобразование для каждой составляющей
, причем обратное z-преобразование для каждой составляющей 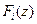 может быть найдено из таблицы
может быть найдено из таблицы 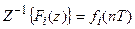 , тогда получаем
, тогда получаем
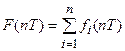 .
.
Для представления сложной дробно-рациональной функции в виде суммы простейших составляющих используются формулы разложения. Например, пусть изображение F(z) представляет собой отношение двух полиномов
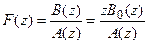 ,
,
При этом предполагается, что степень полиномов числителя не выше степени полинома знаменателя и корни знаменателя простые. В этом случае справедлива такая зависимость:
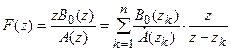 ,
,
где 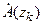 - производная по параметру z;
- производная по параметру z;
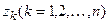 - корни полинома знаменателя.
- корни полинома знаменателя.
Учитывая, что элементарному слагаемому 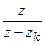 соответствует оригинал
соответствует оригинал 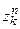 , искомый оригинал можно представить следующим образом:
, искомый оригинал можно представить следующим образом:
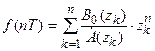 .
.
2. Посредством формулы обращения для z-преобразования, требующей интегрирования в комплексной области
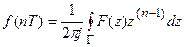 ,
,
причем контур интегрирования Г должен охватывать все полюса функции 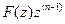 .
.
3. Посредством разложения функции F(z) в ряд по степеням z-1 (ряд Лорана). Если два первых способа аналогичны способам, применяемым в теории преобразования Лапласа, то третий способ вытекает из определения прямого z-преобразования как операция суммирования ряда и не имеет аналогий в теории преобразования Лапласа непрерывных функций.
Из выражения для z-преобразования имеем
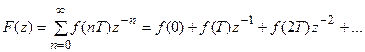 (21.3)
(21.3)
Если теперь функцию F(z) разложить в ряд Лорана (в ряд по степеням z-1), то получим
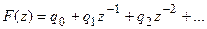 (21.4)
(21.4)
Сравнивая выражения (21.3) и (21.4), находим
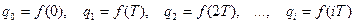 .
.
Таким образом, коэффициенты qi разложения исследуемой функции в ряд Лорана соответствуют дискретам f(iT) функции времени f(t). Такой подход к отысканию оригинала является простым и удобным, поскольку разложение дробно-рациональной функции в ряд по степеням z-1 не вызывает никаких трудностей. Эта операция заключается в делении полинома числителя на полином знаменателя соответствующей дробно-рациональной функции.
2. Определение установившейся ошибки дискретной системы
Установившаяся ошибка дискретной системы при заданном входном воздействии может быть вычислена на основании теоремы о конечном значении. Для замкнутой системы с прерыванием в цепи сигнала ошибки имеем
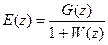 .
.
Полагая систему устойчивой, воспользуемся теоремой о конечном значении
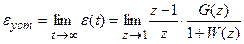 .
.
Рассмотрим определение установившейся ошибки при различных задающих воздействиях для статической и астатической систем.
1. Статическая система. В этом случае для передаточной функции разомкнутой системы имеем 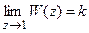 .
.
Для задающего воздействия 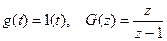 ,
,
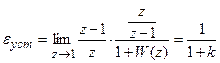 .
.
Для задающего воздействия 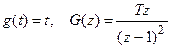 ,
,
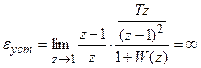 .
.
Для задающего воздействия  ,
,
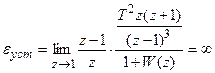 .
.
2. Астатическая система 1-го порядка. Имеем:
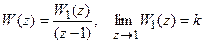 .
.
Для задающего воздействия 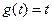
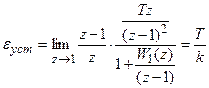 .
.
Для задающего воздействия 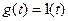
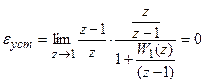 .
.
Для задающего воздействия 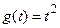
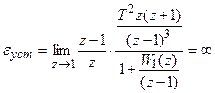 .
.
3. Астатическая система 2-го порядка. Имеем:
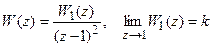 .
.
Для задающего воздействия 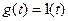
 .
.
Для задающего воздействия 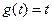
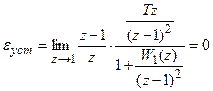 .
.
Для задающего воздействия 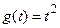
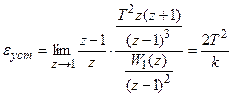 .
.
Как видно из полученных выражений, с увеличением коэффициента передачи разомкнутой системы k установившаяся ошибка уменьшается, но при этом необходимо иметь в виду, что с увеличением этого коэффициента ухудшается устойчивость системы.
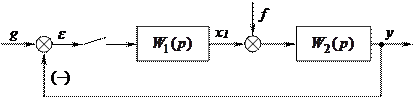 |
Рис. 21.1
Отметим влияние возмущающего воздействия на точность системы в установившемся режиме. Для дискретной системы, изображенной на рис.21.1, имеем
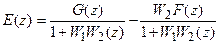 ,
,
поэтому получаем
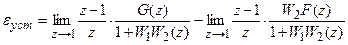 .
.
В общем случае передаточная матрица многомерной дискретной системы относительно сигнала ошибки имеет вид:
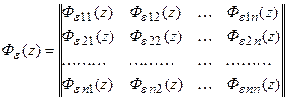 ,
,
где 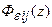 - передаточная функция относительно ошибки по i-му выходу от j-го входа.
- передаточная функция относительно ошибки по i-му выходу от j-го входа.
Очевидно,
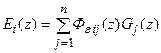 ,
,
тогда
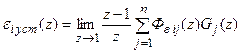 .
.
3. Особенности синтеза дискретных систем управления
При синтезе дискретных систем широко используется математический аппарат, разработанный для импульсных систем. В этом случае цифровая система заменяется эквивалентной структурной схемой цифровой системы (это некоторая нелинейная импульсная цепь).
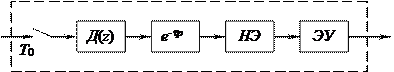 |
Рис. 21.2
Здесь:
Д(z) - дискретный фильтр с передаточной функцией Д(z), которая определяется z-преобразованием разностного уравнения, описывающего алгоритм работы ЦВМ.
e-tp - элемент запаздывания с передаточной функцией e-pt. Элемент запаздывания вводится для учета времени прохождения сигнала через дискретный фильтр.
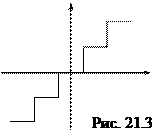 НЭ - нелинейный элемент в виде многоступенчатой релейной статической характеристики, которая учитывает нелинейный эффект квантования по уровню выходных сигналов машины.
НЭ - нелинейный элемент в виде многоступенчатой релейной статической характеристики, которая учитывает нелинейный эффект квантования по уровню выходных сигналов машины.
ЭУ - экстраполирующее устройство - для преобразования дискретного сигнала (числовой код) в непрерывный, значения которого в дискретные моменты времени в каком то смысле близки к значениям числового кода.
Замена цифровой системы эквивалентной системы линейной импульсной системой позволяет использовать для изучения цифровых систем хорошо разработанный аппарат теории линейных импульсных систем. Такой подход предполагает включение следующих условий:
- входные и выходные сигналы цифровой системы квантованы только по времени;
- ЦВМ осуществляет только линейной преобразование входных сигналов;
- логическая схема алгоритма переработки информации не содержит логических условий.
Динамические свойства замкнутых цифровых систем определяются:
- динамическими свойствами непрерывной части системы;
- алгоритмом переработки информации в ЦВМ (законом управления);
- техническими характеристиками ЦВМ и способом ее включения в замкнутый контур.
Экстраполяторы нулевого порядка или фиксирующие устройства запоминают значения сигнала на каждом интервале T0, т.е. на каждом такте прерывания.
В общем случае эквивалентная структурная схема цифровой системы при включении ЦВМ в цепь сигнала ошибки имеет вид
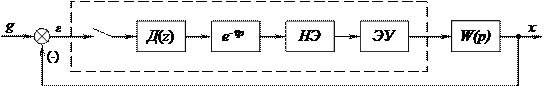 |
Рис. 21.4
Без учета влияния эффекта квантования нелинейный элемент из структурной схемы исключается и цифровая система сводится к линейной импульсной системе.
Рассмотрим экстраполятор нулевого порядка
 |
Рис. 21.5
Импульсная переходная функция экстраполятора нулевого порядка
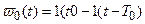 ,
,
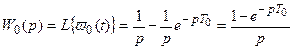 .
.
Эквивалентная структурная схема цифровой системы будет иметь вид:
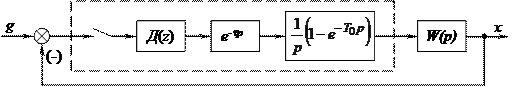 |
Рис. 21.6
Здесь экстраполятор 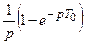 и непрерывная часть образуют в совокупности так называемую приведенную непрерывную часть (ПНЧ) с передаточной функцией
и непрерывная часть образуют в совокупности так называемую приведенную непрерывную часть (ПНЧ) с передаточной функцией
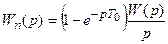
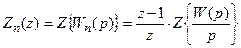
Передаточная функция разомкнутой системы имеет вид
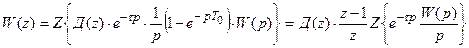
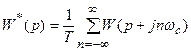 .
.
Для частотных характеристик получаем 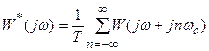 ,
,  .
.
 Частотные характеристики строят
Частотные характеристики строят 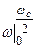 ;
; 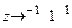 .
.
Д(z) - z-передаточную функцию дискретного фильтра получают из соответствующего уравнения в конечных разностях.
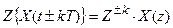 .
.
Билинейное преобразование 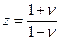 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Анализ линейных дискретных СУ | | | Общая характеристика нелинейных систем |
Дата добавления: 2015-12-11; просмотров: 1223;
