Мода случайной величины.

Модой ( 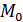(X)) случайной величины называется наиболее вероятное ее значение, то есть значение, вероятность которого максимальна.

Если максимальные вероятности принимают несколько значений случайных величин, то такое распределение называется полимодальным.

Пример.

Дискретная случайная величина X задана законом распределения:

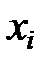
	‒1
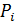
	0,1	0,2	0,1	0,6

Найти: числовые характеристики случайной величины:M(X),D(X),Ϭ(X), 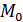(х).

Решение:

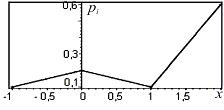
Построим многоугольник распределения данной случайной величины.

1. Математическое ожидание:

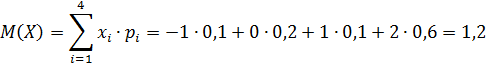
2. Дисперсия:

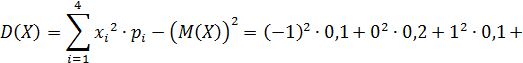
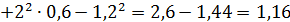
3. Средне квадратическое откланение:

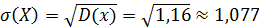
4. 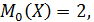так как максимальная вероятность этого значения равна 0,6.

Лекция 6. НАЧАЛЬНЫЕ И ЦЕНТРАЛЬНЫЕ МОМЕНТЫ.

Начальным моментом k‒го порядка называется математическое ожидание k‒й степени случайной величины.

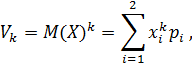
при k=1;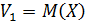

Центральным моментом 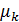случайной величины (X) называется математические ожидание k‒й степени отклонения случайной величины (Х) от ее математического ожидания.

,

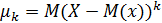при k=2, 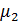=D(Х).