Лекция 5. ПОНЯТИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫ И ЕЕ ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ.
1. Понятие случайной величины.
2. Дискретная случайная величина и законы распределения.
3. Математическое ожидание случайной величины и его свойства.
4. Дисперсия и её свойства.
Под случайной величиной, связанной с некоторым испытанием, понимается всякая величина, которая при осуществлении испытания принимает то или иное числовое значение.
Дискретной случайной величиной называется случайная величина, которая принимает отдельные, изолированные друг от друга, значения с определенными вероятностями.
Законом распределения дискретной случайной величины называется соответствие между всеми возможными значениями случайной величины и их вероятностями.
Случайные величины обозначаются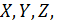 
а их возможные значения соответственно, 
.
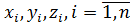Закон распределения случайной величины Х может иметь вид:
1) Ряд распределения случайной величины
| X |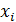 
| 
| 
| … | 
|
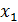
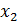
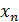
| P |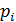 
| 
| 
| … | 
|
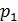
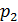
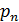
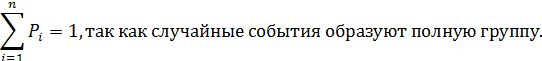
2) Многоугольник распределения
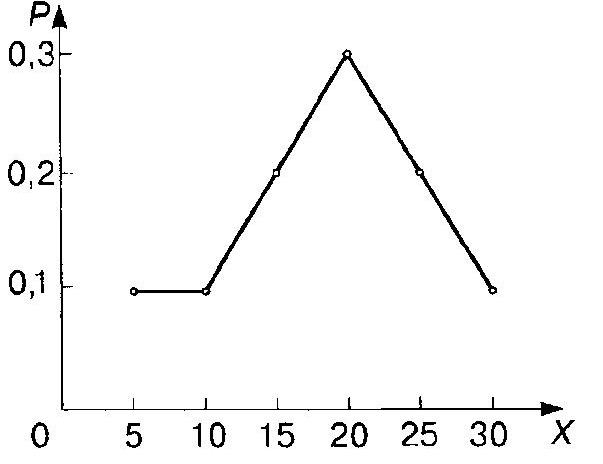
По оси х‒ откладывается значения случайной величины, а по оси у‒ их вероятности.Соединив их ломанной, получим многоугольник распределения.
Дата добавления: 2015-12-16; просмотров: 1053;