Плотность распределения вероятностей непрерывной случайной величины
Рассмотрим интервал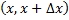 
и определим вероятность того, что непрерывная случайная величина примет значения, заключённые в этом интервале. Согласно свойству 2 имеем 
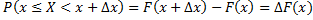. Разделим эту величину на ширину интервала 
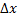, получим величину вероятности, приходящейся на единицу длины интервала: 
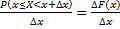, которую назовём средней плотностью распределения вероятности на интервале 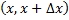. Введём понятие плотности распределения вероятности в данной точке 
, определив её как предел средней плотности на интервале при условии, что 
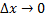и указанный предел существует. Обозначим эту плотность распределения вероятностей через 
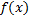, тогда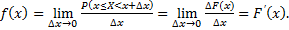 
Плотностью распределения вероятностей непрерывной случайной величины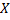 
называют функцию 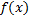- первую производную от функции распределения 
:
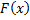Зная плотность распределения 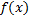, можно найти функцию распределения 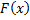. А именно 
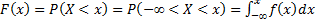. Таким образом:
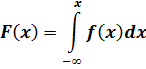
Заметим, что закон распределения непрерывной случайной величины может быть задан как функцией распределения, так и плотностью распределения. Для дискретной случайной величины имеет смысл только функция распределения вероятностей (почему?).
Найдём вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу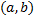 
. 
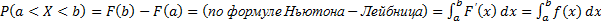. Итак
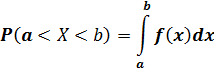
Плотность распределения обладает следующими свойствами:
1. 
.
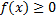2. 
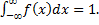
В частности, если все возможные значения случайной величины принадлежат интервалу 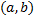, то
.
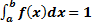Из дифференциального исчисления известно, что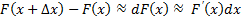 
. Так как 
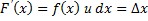, получим
.
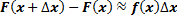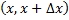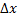Последнее выражение означает: вероятность того, что случайная величина примет значение, принадлежащее интервалу , приближённо равна произведению плотности вероятности в точке на длину интервала . В этом заключается вероятностный смысл плотности распределения.
Дата добавления: 2015-12-29; просмотров: 810;