Числовые характеристики непрерывных случайных величин
Понятие математического ожидания и дисперсии дискретной величины могут быть распространены на непрерывную случайную величину. Только при этом вероятность того, случайная величина примет данное значение 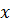 , следует заменить на вероятность попадания случайной величины в бесконечно малый интервал шириной
, следует заменить на вероятность попадания случайной величины в бесконечно малый интервал шириной 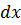 , а суммирование – интегрированием. Из определения функции распределении следует
, а суммирование – интегрированием. Из определения функции распределении следует 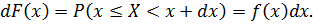 Умножая на
Умножая на 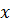 и интегрируя от
и интегрируя от 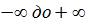 , получим следующую формулу, определяющую математическое ожидание непрерывной случайной величины:
, получим следующую формулу, определяющую математическое ожидание непрерывной случайной величины:
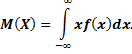
при условии, что несобственный интеграл сходится.
Математическим ожиданием непрерывной случайной величины 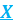 , возможные значения которой принадлежат отрезку
, возможные значения которой принадлежат отрезку 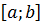 , называют определённый интеграл
, называют определённый интеграл
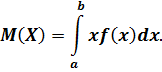
Дисперсией непрерывной случайной величины называют математическое ожидание квадрата её отклонения. Если возможные значения 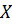 принадлежат отрезку
принадлежат отрезку 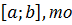
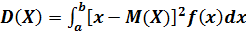 .
.
При решении задач часто пользуются преобразованной формулой дисперсии. А именно 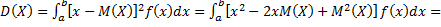
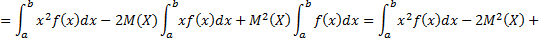
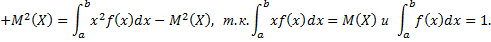
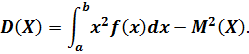
Дата добавления: 2015-12-29; просмотров: 641;
