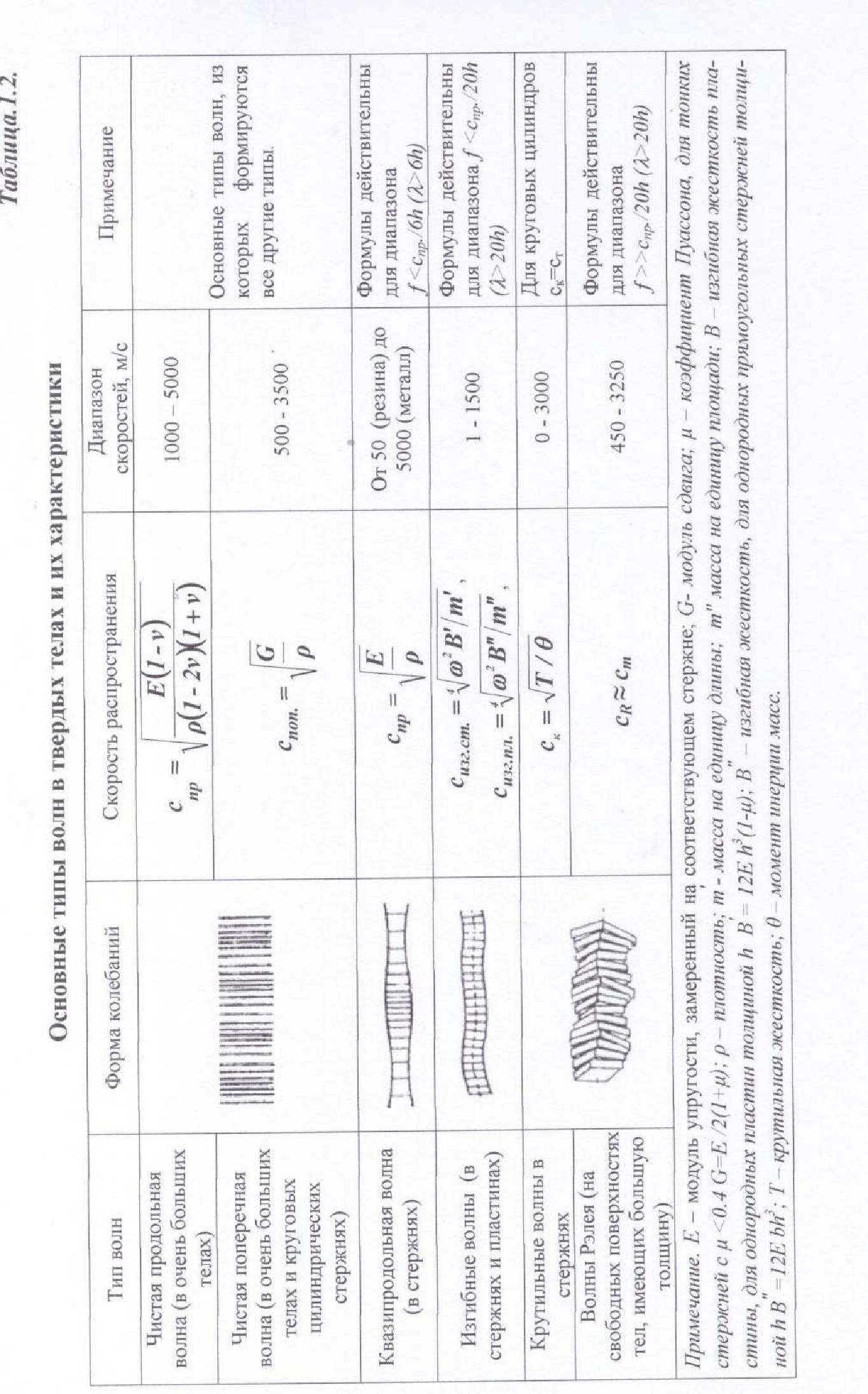
Акустические поля и их характеристики.

Совокупность распространяющихся звуковых волн образует акустиче-ское (звуковое) поле источника звука. При описании акустических полей ис-пользуют понятие фронт волны, который определяется как геометрическое ме-сто точек, колеблющихся в одной фазе (при этом амплитуды не обязательно должны быть равными). В зависимости от вида поверхности, огибающей фронт волны, различают поля плоских, сферических и цилиндрических волн.

Поле плоских волн возникает в трубах и каналах, когда их поперечные размеры малы по сравнению с длиной. Полем плоских волн можно считать и часть акустического поля источника звука на расстоянии много меньше, чем его размеры. В неограниченном пространстве источником плоских волн может быть лишь бесконечная колеблющаяся пластина.

Сферические волны распространяются от точечного источника, пульси-рующей сферы, закрепленной в экране колеблющейся мембраны. Примером та-ких источников могут быть небольшие по сравнению с длиной волны твердые тела, громкоговоритель в экране, отверстие в ограждении, через которое прохо-дит звук.

Поле цилиндрических волн создается при колебании независимых источ-ников звука, расположенных вдоль протяженной линии. Примером могут слу-жить: пульсирующий цилиндр, щель, транспортные пути с потоком движуще-гося транспорта, длинные промышленные установки с большим числом неко-герентно работающих механизмов

Возмущение среды, вызванное источником звука, сопровождается коле-банием частиц среды, изменением ее плотности, температуры, давления. Их значения изменяются как во времени, так и в пространстве. В большинстве слу-чаев процесс происходит почти адиабатически и без существенных изменений плотности среды (исключая нелинейные процессы: взрыв, переход через звуко-вой барьер и т.п.).

Поэтому плотность – ρ (кг / м³) и температура Т (^оК ) принимаются по-стоянными величинами. Основными характеристиками акустических полей яв-ляются: звуковое давление p (Па), определяемое как разность давлений в воз-мущенной и невозмущенной среде; и колебательная скорость частиц среды – υ (м / с).

Поскольку мгновенные значения давления и скорости колеблются отно-сительно среднего значения, то эти переменные принято оценивать эффектив-ными значениями ^~p и υ^~ , которые эквивалентны среднеквадратическим зна-чениям по времени

~
/		(1.14)
р = p_m
~
/	(1 .15)
υ = υ_m

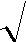
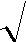где р_m и υ _m – максимальные значения звукового давления и виброскорости. В дальнейшем, для удобства записи, будем обозначать среднеквадратические значения указанных величин без волнистой черты.

Для плоских и квазиплоских звуковых волн, например, при распростра-нении звука в открытом пространстве на некотором расстоянии от источника справедливо следующее соотношение между звуковым давлением и колеба-

тельной скоростью
	р = υ ρ с	(1.16)
Возвратно-поступательное движение частиц среды при распространении
звуковых волн можно охарактеризовать их величиной их смещения ξ	(м), а
также колебательным	ускорением а (м /с²). Эти параметры наряду с колеба-
тельной скоростью υ	чаще всего используются для описания процесса распро-

странения звука в твердых средах и потому υ и а принято называть виброско-ростью и виброускорением.

Помимо указанных выше параметров акустических полей в различных средах для характеристики их свойств вводят понятие акустического импедан-са или акустического сопротивления Z. Он определяется отношением звуко-вого давления и колебательной скорости частиц

Z = p , (Н^.с/м³) (1.17)

υ

Из (1.16) следует, что в поле плоских или квазиплоских звуковых волн выражение для импеданса принимает простую форму

Z = ρ c (1.18)

В поле сферических или цилиндрических волн аналогичное выражение для волнового сопротивления справедливо лишь на значительном удалении от источника, т.е. там, где кривизна фронта волны будет столь мала, что ее можно считать плоской. Это выполняется на расстояниях вдвое превышающих длину волны, т.е.

r ≥ 2 λ (1.19)

В твердых средах и телах величина волнового сопротивления для попе-речных и продольных волн будет различной в силу отличия значений скорости распространения соответствующих волн.

Из (1.18) видно, что акустическое сопротивление зависит лишь от плот-ности среды и от скорости распространения звука в ней. В табл. 1.1 приведены значения акустических сопротивлений для различных сред и материалов. В следующих разделах будет показано, что соотношение акустических сопротив-лений сред определяет процессы прохождения и отражения звуковых волн на их границе.

Энергетической характеристикой акустического поля является его ин-тенсивность (сила звука) I (Вт/м²), которая определяется потоком энергиипроходящей через единичную площадку за единицу времени. Величина интен-сивности определяется через звуковое давление и виброскорость из соотноше-ния

I = p( t)⋅υ(t) = ( p_m ⋅υ_m ) / 2 (1.20)

Здесь черта сверху обозначает осреднение по времени.

Используя (1.14 – 1.18) можно записать для поля плоских и квазиплоских

волн:

I = р_m υ_m / 2 = p² / ρc = p²/ Z = υ² ρc = υ² Z (1.21)

Следует отметить полезное следствие, вытекающее из (1.21). Интенсив-ность звука I по определению является векторной величиной. Измерение таких физических величин, как известно, представляет определенные трудности, т.к. результат зависит от ориентации приемника излучения. Из вышеприведенной формулы следует, что по измерениям звукового давления р, являющегося ска-лярной величиной, можно найти величину интенсивности звука.

По интенсивности звука можно определить количество энергии, излучае-мой источником звука, т.е. акустическую мощность источника W (Вт). Для ис-точника плоских волн эта величина определится умножением интенсивности I на площадь сечения S, в котором излучается звуковая энергия, т.е. W = I^.S.

Звуковая мощность как характеристика источника довольно часто соот-носится с механической или электрической мощностью Р_m источника. В этом случае может быть введено понятие акустического коэффициента полезного действия ζ =W/Р_m, некоторые ориентировочные значения которого приведены в табл.1.3. Акустический КПД используется для приближенного определения звуковой мощности.

Таблица 1.3.

<123 4 5 6 7 >

Дата добавления: 2016-01-03; просмотров: 5632;