Звук и звуковые волны.
ПРОМЫШЛЕННАЯ
АКУСТИКА
Цели курса: освоение основных закономерностей возникновения звуковых
волн и процессов их распространения в различных средах, а также формирования акустической интуиции, что необходимо для работы в области прикладной акустики, в частности – промышленной акустики, занимающейся методами идентификации источников шума и подавления звукоизлучения промышленного оборудования.
1 . О С Н О В Ы О Б Щ Е Й А К У С Т И К И
Акустика – наука о закономерностях возникновения и распространениязвуковых волн в газообразных, жидких и твердых средах.
Как и большинство других основ науки акустика ведет свое начало из древней Греции. Известно, что уже Пифагор, изучая звучание струнных инст-рументов, проводил опыты с натянутой струной, для чего придумал специаль-ное устройство монохорд (натянутая на деку струна с передвижными колками),
с помощью которого он изучал влияние длины струны на издаваемый ею звук. Его последователями в изучении тайн звука были древнегреческие ученые-исследователи: Аристоксен, Архелай, Зенон, Хрисипп, Диоген Вавилонский. В своих работах они утверждали, что "воздух между слушателями и звучащим предметом колеблется кругами, а затем расходится волнами, как вода в водоеме от брошенного камня". Таким образом, уже древние греки рассматривали звук как колебательный процесс.
Основы классической акустики были заложены Галилео Галилеем, ис-следовавшим, как и Пифагор, процесс извлечения звука в результате колебания твердых тел (струн и пластин). В начале 19 века Гюйгенс исследовал процесс распространения волн. Ньютоном в его важнейшем труде "Математические на-чала натуральной философии" были разработаны основы волновых процессов в разных средах. Им было введено понятие длины волны, выведена формула для определения скорости звука.
Большой вклад в акустические исследования был внесен экспериментами
с колеблющимися твердыми телами, которые проводили Л. Эйлер, Э. Хладни, Ф. Савар. Во второй половине 19 века фундаментальные теоретические работы были независимо выполнены Г. Гельмгольцем и лордом Рэлеем. Трактат Рэлея "Теория звука" до настоящего времени является основополагающим фундамен-том акустики.
Применение методов прикладной математики позволило построить стройную теорию звука не только для воздушной, но и для жидких и твердых сред, что нашло отражение в ставших уже классическими трудах Лайтхилла, Скучика, Тейлора, Блохинцева, Мунина, Голдстейна.
Развитие акустики связано с развитием экспериментальной техники и расширением области практических применений. В зависимости от направле-ния и задач исследований известны следующие направления современной аку-стики:
музыкальная акустика (извлечение звука музыкальным инструментами и его распространение в воздухе);
строительная и архитектурная акустика (распространение звука в звуко-проводах, помещениях, по строительным конструкциям);
гидроакустика (передача звука в водной среде); биоакустика (звуковые волны, излучаемые живыми объектами); молекулярная акустика;
ультраакустика (использование ультразвука для исследований материа-лов, в том числе для акустодиагностики);
авиационная акустика (звуковые волны, создаваемые газовыми струями, летательными аппаратами);
учение о гиперзвуке; акустодиагностика (в машиностроении, неразрушающем контроле, в ме-
дицине); техническая акустика (звукоизлучение и распространение звуковых волн,
создаваемых машинами и оборудованием).
Задачи акустики – изучение закономерностей процессов:звукоизлучения различными источниками; распространения звуковых волн в воздушной, жидкой, твердой и пла-
стичной средах, в однородных и слоистых средах; дифракции и интерференции звука.
Методы акустики: экспериментальный и теоретический.
Как следует из приведенных выше кратких сведений об этапах развития акустики, первичным являлся экспериментальный метод, основанный на про-ведении опытов с реальными колеблющимися средами в конкретных условиях. Именно результаты этих экспериментов позволили сделать первые выводы о физической природе звука и закономерностях его излучения и распростране-ния.
Теоретический метод основан на том, что наука о звуке трактуется каксвоеобразная механика упругих волн, в которой изучается поведение волн, как самостоятельных объектов, в отличие от обычной механики, занимающейся по-ведением материальных тел.
Основные понятия и определения
Звук и звуковые волны.
Звук – колебания частиц упругой среды (газообразной, жидкой или твер-дой), возникающие при ее динамическом возмущении. В твердых средах по-добные колебания принято называть звуковыми вибрациями.
Причинами динамических возмущений среды может быть действие меха-нических или электромагнитных сил, изменение термодинамических парамет-ров среды: плотности ρ, давления p, температуры T. В соответствие с этим раз-личают звуки механического происхождения (колебания пластин, мембран, струн, звук удара), электромагнитного происхождения (гудение трансформа-тора, электрических машин) и аэрогидродинамического происхождения (звук в трубах и каналах, звук выпуска струй газа или жидкости, звук насосов и венти-ляторов, звук реактивных двигателей, гудение пламени).
Возникшее в какой-либо точке среды возмущение вызывает ее деформа-ции, в результате которых в колебательное движение вовлекаются вначале близлежащие, а затем и удаленные частицы среды. Энергия, излучаемая источ-ником звука, распространяется в виде звуковых волн.
Вследствие различия свойств жидких, газообразных и твердых сред, имеются некоторые особенности распространения в них звуковых волн.
В жидких и газообразных средах возможны лишь деформации сжатия-растяжения и поэтому возмущения в них распространяются только в направле-нии колебания частиц среды. Образующиеся при этом звуковые волны называ-ются продольными.
В твердых средах помимо деформаций сжатия-растяжения возможны де-формации сдвига. Смещения частиц среды происходят здесь как в продольном, так и в поперечном направлении. В связи с этим, возможно распространение как продольных, так и поперечных волн, в которых направление распростране-ния волны перпендикулярно направлению колебания частиц.
В чистом виде ни поперечные, ни продольные волны в твердых телах не существуют. Но, на основании теории упругости, всякое волновое движение можно представить в виде суммы продольных и поперечных волн. На практике
в реальных телах чаще всего встречаются следующие типы волн: Квазипродольные – волны, распространяющиеся в стержнях вдоль оси.
Вследствие поперечного сжатия возникают смещения частиц среды, перпенди-кулярные направлению распространения волн. В результате скорость их рас-пространения уменьшается по сравнению со скоростью чисто продольных волн. Это различие особенно велико для резиноподобных материалов;
Изгибные – волны, в которых колебания частиц происходят перпенди-кулярно как к направлению их распространения, так и к поверхности твердого тела. Волны этого типа присутствуют в пластинах и стержнях. Именно они вно-сят наибольший вклад в звукоизлучение колеблющихся конструкций из пла-стин и стержней;
Волны Рэлея – поверхностные волны в твердых телах, имеющих боль-шую толщину (массивные плиты, фундаменты, земная кора). Особенностью этих волн является быстрое убывание (по экспоненте) их амплитуды с продви-жением вглубь тела.
Звуковые вибрации в твердых телах вызывают смещения частиц окру-жающей воздушной среды, расположенных в непосредственной близости от их поверхности. Таким образом, энергия колебания частиц твердой среды переда-
ется частицам воздушной среды. Возникающий при этом звук принято назы-вать воздушным.
Следует заметить, что возможно и обратное воздействие воздушного зву-ка на твердые поверхности (передача колебательной энергии на пластины, пе-регородки, перекрытия и пр.).
В акустике принято распространяющиеся звуковые волны представлять в виде суммы гармонических волн. Это позволяет получить решения для боль-шинства задач, касающихся процессов распространения, излучения, отражения
и поглощения звуковых волн. Таким образом, разложение на гармонические волны позволяет применить хорошо разработанный математический аппарат.
Звуковые волны характеризуются длиной волны λ (м); частотой f (Гц);
и скоростью звука (скорость распространения волн) с (м/с). Между этими ха-рактеристиками существует известная зависимость
| λ = с / f | (1.1) |
Иногда удобно пользоваться величиной угловой частоты колебаний
| ω = 2 π f | (1.2) |
В уравнениях теории звука часто встречается величина, называемая вол-новым числом, которое определяется как
| k = ω / c = 2π f / c = 2π / λ | (1.3) |
Слышимый диапазон частот располагается в интервале от 16 Гц до 20 кГц. Колебания с частотами ниже указанного интервала называются инфразву-ком, с более высокими частотами - ультразвуком.
Пример: рев быка – 30 Гц; писк комара – 10 кГц.
Скорость звука зависит как от типа волн, так и от механических свойств среды. В газообразных средах
| с = | γ p / ρ | (1.4) |
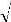
где γ = ср/ сυ– отношение удельных теплоемкостей при постоянном давлении и постоянном объеме (для воздуха γ = 1,4); р – давление газа; ρ – плотность среды.
В широком диапазоне температур справедливо известное соотношение
| с = | γRT/µ | (1.5) |
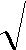
здесь R– газовая постоянная; Т – абсолютная температура газа, оК; µ – моле-кулярный вес газа.
С учетом этого для воздуха при температуре tоС
| с = 332 + 0,6 t , | (1.6) | ||
| где 332 м/с – скорость звука при 0 о С. | |||
| Для жидкостей скорость звука можно определить по формуле | |||
| с = | K / ρ | (1.7) | |
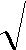
где К – модуль упругости среды – величина обратная сжимаемости среды β, (К
= 1/ β)
В табл. 1.1. приведены скорости звука в некоторых газах и жидкостях.
| Таблица 1.1. | |||
| Скорость звука в газах и жидкостях (при температуре 20оС) | |||
| Наименование газа или | Плотность | Скорость звука | Акустическое |
| жидкости | ρ, кг/м3 | с, м/с | сопротивление ρс, кг/м2 с |
| Водород | 0,084 | ||
| Гелий | 0,167 | ||
| Кислород | 1,34 | ||
| Азот | 1,17 | ||
| Окись углерода | 1,17 | ||
| Углекислый газ | 1,85 | ||
| Воздух | 1,21 | ||
| Водяной пар (130оС) | 0,54 | ||
| Бензин | 89.104 | ||
| Вода дистиллированная | 149.104 | ||
| Глицерин | 246.104 | ||
| Кислота соляная | 136.104 | ||
| Толуол | 115.104 |
При практических расчетах можно принимать скорость звука в воде и в жидких топливах ≈ 1500 м /с.
В твердых телах большое значение имеет тип распространяющихся волн,
а также свойства материала и размеры тел. Продольные и поперечные волны распространяются с различной скоростью, что объясняется различием величи-ны возникающих в среде деформаций сжатия и сдвига. Очевидно, что при од-ной и той же частоте колебаний длины волн поперечных и продольных будут отличаться.
В безграничных средах скорость распространения продольных волн
| Cпр = | E(1 - ν) | (1.8) | |
| ρ(1 - 2ν)⋅(1 + ν) |

где Е – модуль Юнга; ν – коэффициент Пуассона;
ρ – плотность материала среды.
В тонких стержнях, поперечные размеры которых меньше длины про-дольной волны, распространяются квазипродольные волны, скорость которых
| Cпр = | Ε | (1.9) | |||
| ρ | |||||
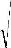
Для высокочастотных колебаний или для широких стержней, когда длина волн в несколько раз меньше поперечных размеров стержня, скорость распро-странения продольных волн, с достаточной точностью, определяется по форму-ле (1.8), т.е. стержень рассматривается как безграничная среда. В металличе-ских стержнях различие этих скоростей будет невелико (для большинства ме-таллов ν≈ 0,3). В то же время для резиноподобных материалов, для которых коэффициент Пуассона ν близок к 0,5 , величина (1-2ν), стоящая в знаменателе (1.8) стремится к нулю и, следовательно, скорость продольных волн в безгра-ничной среде или широких стержнях будет во много раз превышать скорость в
тонких стержнях. Этот факт имеет большое значение при решении задач виб-роизоляции.
Скорости поперечных волн, обусловленных деформациями сдвига, суще-ственно зависят от частоты колебаний f и от формы тела. В стержнях и пла-стинах такие волны называются изгибными. Скорость их распространения в пластинах
| ⋅ 4 | ⋅ 4 | , | ||||||||
| сизг.ст. = | 2ππ | D/M | = | 2πf | EJ / ρh(1 −ν 2 ) | (1.10) |
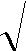
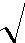
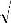
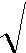
Eh3
где D =– изгибная жесткость пластины; M = ρh – масса на единицу
12 (1 − ν2)
ширины пластины; J = h3/ 12 – момент инерции на единицу ширины пластины; h – толщина пластины.
Для изгибных волн в стержнях
| сизг.ст. = | EJст. | ≈ 1,35 | , | ||||||
| 2π ⋅ f | ⋅ 4 | сст.hf | (1.11) | ||||||
| ρS |
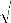
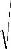
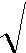
где S – площадь поперечного сечения стержня; сст. – скорость продольных волн в стержне; Jст. = bh3/ 12 - момент инерции поперечного сечения стержня
(b).
В стальных пластинах и стержнях с достаточной точностью величину скорости изгибных волн можно определить по формуле:
| сизг. ≈ 950 hf | (1.12) |
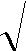
В больших телах и круговых цилиндрах скорость поперечных волн не зависит от частоты и может быть представлена в виде
| споп. = | G | (1.13) |
| ρ |
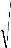
где G – модуль сдвига.
В табл. 1.2. приведены характеристики основных типов волн и их полей в твердых телах.
Дата добавления: 2016-01-03; просмотров: 2522;
