Излучение звука простейшими источниками.
Передача энергии звуковых колебаний от твердых тел окружающей среде представ-ляет собой довольно сложный физический процесс, эффективность которого существенно зависит не только от соотношения акустических сопротивлений, но и в значительной степе-ни от формы и размеров колеблющегося тела. Задача звукоизлучения требует решения сис-темы дифференциальных уравнений, описывающих волновые процессы в средах с разными свойствами. Как известно, для получения точных решений необходимо знать граничные ус-ловия. Кроме того, точное решение возможно лишь для относительно простых случаев, не-которые из которых и будут рассмотрены ниже (рис.1.6).
| а) | б) | в) | |
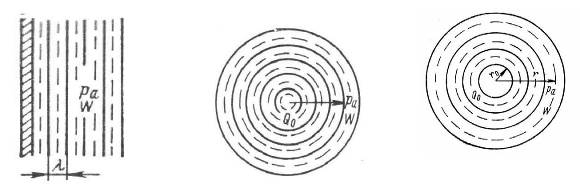
а – протяженная синфазно колеблющаяся пластина; б – точечный источник;
в – пульсирующая сфера
Рис. 1.6. Излучение звука простейшими источниками.
Протяженная (по сравнению с длиной волны) пластина, все точки по-верхности которой совершают синфазные поперечные колебания, создает поле плоских волн (рис.1.6, а). На границе со средой колебательные скорости пла-стины и частиц среды равны, поскольку в случае поперечных колебаний пла-
стины вся колебательная энергия передается частицам воздушной среды, на-правление колебаний которых совпадает с направлением распространения зву-ковых волн. При этом звуковое давление в среде прямо пропорционально ко-лебательной скорости независимо от частоты. Источник такого типа считается наиболее эффективным. Можно показать, что в этом случае уровень колеба-тельной скорости поверхности пластины (виброскорость) будет равен уровню звукового давления, измеренного в непосредственной близости от пластины, т.е. Lυ= L. Примером реального источника такого типа могут служить толстые металлические плоские стенки картера двигателя в диапазоне высоких частот, когда длина волны в воздухе мала.
Менее эффективным излучателем звука является точечный источник (рис.1.6, б ). Таким источником является синфазно пульсирующая сфера, ради-ус которой существенно ниже длины волны (rо<<λ). При этом формируется пое сферических волн. Звуковое давление на частоте f и интенсивность звука на расстоянии r <<λ можно найти по формулам
| р = Q ρ f / 2 r | (1.51) |
| I = p2 / 2ρc = Q2ρf / 8 c r2 = k2 Q2ρc / 32 π2 r2 | (1.52) |
где Q = 4π rо2*υ — производительность источника или амплитуда объемной скорости источника; k = ω/с - волновое число.
Акустическая мощность W такого источника, называемого монополь оп-ределяется по его производительности
| W = 4πr2I = πf2Q2ρ / 2ρ = k2 Q2ρc / 8π | (1.53) |
Как видно из вышеприведенной формулы, акустическая мощность суще-ственно увеличивается с частотой (W~ k2= 2π f2/с2)
Реально такие источники практически не встречаются, но в первом при-ближении небольшие по размеру механизмы можно считать источником типа монополя. Это позволяет значительно упростить расчет акустического поля данного механизма.
Как уже отмечалось в п.1.1.2. , в поле сферических волн фазы звукового давления и колебательной скорости не совпадают. Вследствие этого колеба-тельная скорость в сферической волне, в отличие от давления, характеризуется двумя членами, величины которых по-разному изменяются с расстоянием. Пер-вый из них характеризует собственно акустическую волну и уменьшается об-ратно пропорционально расстоянию, т.е. ~ 1 / r. Второй член, обусловленный реактивной составляющей акустического сопротивления, изменяется ~ 1 / r2, и, следовательно, вносит наибольший энергетический вклад в поле в непосредст-венной близости от источника. Следует отметить, что возмущение среды здесь происходит без ее сжатия. Названные составляющие колебательной скорости уравниваются на расстоянии r = 1 / k = с/2π f, далее начинает превалировать первая, акустическая, составляющая.
При увеличении радиуса пульсирующей сферы rо по мере увеличения расстояния и частоты, когда rо>> λ, реактивная составляющая колебательной скорости частиц среды существенно уменьшается, кривизна фронта волны уменьшается и поле источника можно считать полем плоских волн (рис. 1.6, в).
Следующим простым типом источника является колеблющаяся в беско-нечной среде жесткая сфера, радиус которой rо<< λ. Такой источник называется диполь. Он образуется при работе в противофазе двух одинаковых располо-женных на малом расстоянии d точечных источников, производительностью Q. Интенсивность звука в точке, расположенной на достаточном, по сравнению с длиной волны, расстоянии r в направлении, составляющем с осью диполя угол θ можно определить по формуле
| I = (ρω4M2/ 32π2c3r2) * cos2 θ | (1.54) |
где М = Qd – момент диполя.
Как видно из (1.2.7) источник этого типа излучает звуковые волны нерав-номерно. Максимальное излучение наблюдается в направлении, совпадающем с осью диполя, т.е. с линией соединяющей точечные источники. В перпендику-лярном к центру оси направлении излучение вообще отсутствует. Характери-стика направленности диполя представляет собой восьмерку (рис. 1.8.). Аку-
стическая эффективность диполя зависит от частоты и в целом меньше продук-тивности монополя (Wд/ Wм= k2d / 3). Источникам типа диполя можно считать тело, совершающее возвратно-поступательное движение с небольшой амплитудой, колеблющийся стержень, струна, пропеллер. Причиной возникновения источников этого типа может быть гармоническая сила, приложенная к среде, или несколько гармонических сил, приложенных одновременно к малой по сравнению с длиной волны области среды.
В турбулентных потоках, например в струях истекающего газа, появля-ются источники типа квадруполя, характеристика направленности которых представляет собой две восьмерки с общим центром. В целом квадруполь пред-ставляет собой два диполя с осью d1 , оси которых отстоят друг от друга на рас-стоянии d2. Различают поперечный и продольный квадруполи. В поперечном диполе оси их параллельны друг другу, а в продольном расположены на одной прямой. Акустическая мощность квадруполя определяется по формуле
| Wпрод.кв. = ρсω6(Qd1d2)2 / 40 π с6 | (1.55) |
| Wпоп.кв. = ρсω6(Qd1d2)2 / 480 π с6 | (1.56) |
Как видно из формул квадруполь наиболее эффективен на высоких часто-тах, т.к. его мощность пропорциональна шестой степени частоты. Этот факт яр-ко подтверждается спектром излучения турбулентных струй, которые, как уже отмечалось выше, можно представить в виде совокупности квадруполей.
В таблице 1.6. приведены сводные данные об элементарных источниках, показана акустическая эффективность по сравнению с монополем.
Дата добавления: 2016-01-03; просмотров: 2030;
