Уровень виброускорения
| . | – 2 | (1.35) | ||
| Lа = 10 lg а / ао ; ( ао = 3 *10 | м /с ) |
Из (1.31) и (1.32) с учетом (1.21) следует, что уровень интенсивности и уровень звукового давления совпадают по величине, поскольку I~p2,т.е.
L = 10 lg I / Io = 10 lg p2 / pо2 = 20 lg p / pо = Lp (1.36)
В дальнейшем, говоря об уровне звукового давления, будем опускать ин-декс у знака уровня L.
Уровень акустической мощности, согласно (1.22) и (1.31), определится по формуле
LW = 10 lg W / Wо = 10 lg (I * S / Io * Sо) = 10 lg 10 0.1L +10 lg S / Sо (1.37)
где Sо = 1м2 – площадь поверхности единичной сферы, принимаемая в качестве порогового значения. Следовательно, между уровнями звуковой мощности и давления справедливо следующее соотношение:
| L W = L + 10 lg S | (1.38) |
Очевидно, что уровень звука при увеличении расстояния от источника в n раз будет уменьшаться на величину
∆L = 10 lg (r22 / r12) = 20 lg n, (дБ) (1.39)
При удвоении расстояния ∆L = 20 lg2 = 20 * 0,3 = 6 дБ
Такое же увеличение расстояния от оси источника цилиндрических волн приведет к снижению уровня звука в два раза меньшему, поскольку соглас-но(1.28),
| ∆L = 10 lg (r2 / r1) = 10 lg n | (1.40) |
Сложение акустических величин возможно лишь на энергетическом уровне, т.е. с учетом (1.26) Поэтому следует отметить основные правила дейст-вия с логарифмическими величинами, какими являются уровни звука, звуково-го давления, мощности и пр.
Определим уровень звука, создаваемого рядом источников, каждый из которых создает в данной точке пространство звук, уровень которого составля-ет Li. Для этого вначале определим абсолютные значения интенсивностей. Из (1.32) следует, что
| Ii = 10 0.1 Li | (1.41) |
Сложим их энергетически и вновь прологарифмируем суммарную интенсив-ность
| n | Ii | n | |||
| LΣ = 10 lg ∑ | = 10 lg∑100 ,1Li | (1.42) | |||
| I0 | |||||
| i =1 | i =1 | ||||
Для n источников, создающих равные уровни интенсивности L, суммарный уровень определится как
| LΣ = L + 10 lg n | (1.43) |
Выражение (1.42) для практических целей удобно привести к следующе-му виду
| n | ||
| LΣ = Lmax +∑100 ,1( Li −Lmax ) = Lmax + L | (1.44) | |
| i=1 | ||
| где | Lmax – максимальный из всех Li уровень; | |
| (Li - Lmax ) – разность i–го уровня с максимальным. |
Поскольку (Li - Lmax) всегда будет < 0, то при разности уровней более 10дБ, второе слагаемое в скобках будет существенно < 1, т.к. логарифм выра-жения, стоящего под знаком логарифма, будет близок к нулю и вклад таких ис-точников на суммарном уровне почти не скажется.
| Пример 1 | L1 | = 90 | дБ; | L2 = 90 дБ |
| L∑ = 90 + 10lg2 =90 + 10 * 0.3 = 93 дБ | ||||
| Пример 2 | L1 | = 80 | дБ; | L2 = 65 дБ |
| L∑ = 80 + 10 lg (1 + 10-1,5) = 80 + 10 lg ( 1 + 0. 032) = 80 + 10 lg 1.032= | ||||
| = 80 + 0.14 ≈ 80дБ | ||||
| Пример 3 | L1 | = 80 дБ; | L2 = 75 дБ; L3 = 70 дБ |
L∑ = 80 + 10 lg (1 + 10-0,5 + 10-1 ) = 80 + 10 lg ( 1 + 0. 32 + 0.10 ) = = 80 + 10 lg 1.42 ≈ 80 + 1.5 ≈ 81.5 дБ
Ниже приводится таблица, составленная для ∆L и позволяющая легко оп-ределить суммарный уровень звука, создаваемого несколькими источниками.
| (Lmax - Li ), дБ | |||||||||||||
| ∆L= 10 lg (1 + 100.1(Li – Lmax)) | 2,5 | 1,8 | 1,5 | 1,2 | 0,8 | 0,6 | 0,5 | 0,4 | 0,2 |
Следуя правилу сложения уровней можно по разности уровней опреде-лить, как изменяется интенсивность звуковых волн. Пусть изменение уровня составляет N дБ, тогда очевидно
| N = L2 – L1 = 10 lg I2 / I1 и I1 /I2 = 10 0,1 N | (1.45) |
Прирост уровня на 1 дБ соответствует увеличению интенсивности в 1,26 раза (100,1 ≈ 1,259), что практически не ощутимо на слух. В тоже время точ-ность акустических расчетов и измерений не превышает 0,1 дБ, что соответст-вует погрешности по интенсивности не более 2% (100,01≈ 1,02 т.е. = 0.02 ). По-этому неправомерно при проведении замеров и расчетов указывать значения
уровней акустических величин или их разностей с более высокой точно-стью.
1.1.4. Звуковые спектры. Октавные и 1/3-октавные полосы частот
При решении практических задач чаще всего приходится иметь дело не с чистыми тонами, т.е. звуками одной частоты, а сложными звуками, представ-ляющими собой смесь многих простых колебаний различной интенсивности и частоты. Как известно, сложный колебательный процесс можно представить в виде суммы гармонических функций. Для звукового давления имеем
| р(ω ,t ) =∑ pi ⋅ sin(ωi t + φi | ) =∑ pi ⋅ sin( 2πfi t + φi ) | (1.46) |
| i | i |
где pi, fi ,ωi и φi - соответственно амплитуда, частота круговая частота и фаза составляющих.
Как известно из механики, графическое изображение этого процесса в функции времени называется осциллограммой. Такое представление при необ-ходимости выявления частотных составляющих требует специального гармо-нического анализа. В связи с этим, в акустике принято колебательный процесс изображать в виде функции частоты. Такая запись называется спектрограммой или звуковым спектром. Спектр позволяет судить о том, колебания каких час-
тот вносят наибольший вклад в формирование акустического поля, для каких частот следует проектировать звукоизоляцию и звукопоглощение, какова должна быть эффективность шумозащитных средств.
Различают несколько типов звуковых спектров (рис. 1.1). Спектр, в кото-ром отдельные составляющие отделены друг от друга более или менее значи-тельными частотными интервалами (рис.1.1, а), называется линейчатым илидискретным.
Кратные составляющие линейчатого спектра называются гармониками. Количество и сила отдельных частотных составляющих звука определяют его слуховую окраску – тембр.
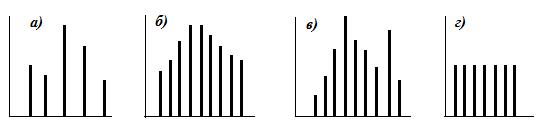
а – линейчатый спектр; б – сплошной спектр; в – смешанный спектр; г – спектр белого шума
Рис.1.1. Типы звуковых спектров
Если частотные составляющие следуют одна за другой непрерывно, то спектр называется сплошным (рис.1.1, б). Такие спектры возникают при соуда-рении тел и при образовании звуковых импульсов. В случае, когда составляю-щие сплошного спектра шума имеют равные амплитуды (рис.1.1, г) шум назы-вают белым шумом.
Человеческое ухо различает частотные составляющие звуковых колеба-ний также как и их амплитуды, т.е. по логарифмическому закону. Поэтому при-нято рассматривать и сравнивать частотные составляющие в полосах частот, ширина которых увеличивается по мере увеличения частоты. Общепринятыми считаются октавные и 1/3-октавные полосы частот. Каждая последующая ок-тавная полоса в два раза шире предыдущей, т.е. отношение верхней и нижней
граничных частот равно 2. В 1/3- октавных полосах это отношение равно 3√2.
Частотные полосы обозначаются их центральными частотами, которые опреде-ляются как среднегеометрическая величина верхней и нижней частоты данной
полосы, т.е. f =  √ f1 ⋅ f2 .
√ f1 ⋅ f2 .

В табл. 1.4. приведены центральные частоты и приближенные значения граничных частот октавных и 1/3-октавных полос.
Таблица 1.4.
Центральные и граничные частоты октавных и 1/3-октавных полос частот
| Октавные полосы частот | Третьоктавные полосы частот | |||||
| центральная | нижняя | верхняя | центральная | нижняя | верхняя | |
| частота | частота | частота | частота 1/3- | частота 1/3- | частота 1/3- | |
| октавы f, Гц | октавы f1 , Гц | октавы f2 , Гц | октавы f, Гц | октавы f1 , Гц | октавы f2 , Гц | |
| 16,0 | 14,1 | 17,8 | ||||
| 20,0 | 17,8 | 22,4 | ||||
| 25,0 | 22,4 | 28,2 | ||||
| 31,5 | 31,5 | 28,2 | 35,5 | |||
| 40,0 | 35,5 | 44,7 | ||||
| 50,0 | 44,7 | 56,2 | ||||
| 56,2 | 70,8 | |||||
| 70,8 | 89,1 | |||||
| 100,0 | 89,1 | |||||
| 10 000 | 11 220 | |||||
| 12 500 | 11 220 | 14 130 | ||||
| 16 000 | 11 360 | 22 720 | 16 000 | 14 130 | 17 780 | |
| 20 000 | 17 780 | 22 390 |
При построении спектров в октавных или 1/3-октавных полосах частот используют логарифмический масштаб, как для шкалы уровней, так и для шка-лы частот. Независимо от абсолютной ширины полосы частот, все они изобра-жаются отрезками одинаковой величины. В целом октавный спектр будет пред-ставлять собой гистограмму, состоящую из столбиков одинаковой ширины, вы-сота которых будет зависеть от уровня звуковой энергии всех частотных со-ставляющих, входящих в данную октаву (рис.1.2.).
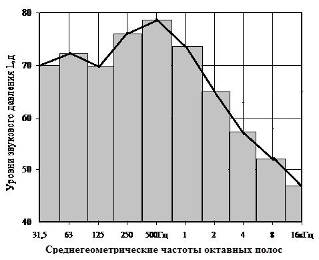
Рис.1.2. Октавный спектр шума Общепринято вместо гистограммы использовать условное изображение
спектра в виде ломанной кривой, координаты точек излома которой определя-ются центральной частотой октавы или 1/3-октавы и уровнем звуковой энергии в данной полосе частот (см. огибающую кривую на рис.1.2). Поскольку такое изображение условно, то интерполяция для определения промежуточных зна-чений в данном случае будет некорректна.
Представление звуковых спектров в полосах частот значительно упро-щает проведение измерений и анализа полученных результатов, поскольку уменьшается их объем и затраты времени. В большинстве случаев достаточно проводить анализ в октавных полосах. Однако, при анализе звуковых вибраций, аэродинамических шумов, а также для тщательного выяснения причин повы-шенных уровней шума, выявления конкретных его источников, проектирования эффективных шумозащитных средств, требуется проведение частотного анали-
за в более узких полосах частот, т.е. в 1/3-октавах, либо в узких полосах с по-стоянной шириной
Если источник создает шум, такой что в каждой полосе частот, независи-мо от ее ширины, излучается одинаковая звуковая энергия, то такой шум назы-вается розовым шумом. Поскольку ширина каждой октавной полосы увеличи-вается вдвое, то интенсивность звука в каждой октаве будет уменьшаться также в два раза. Октавный спектр такого шума будет представлять собой прямую ли-нию.
Для интегральной оценки уровня звука по всему спектру следует вос-пользоваться правилом энергетического сложения (1.42), проводя суммирова-ние уровней звукового давления Li по всем частотным полосам. Очевидно, что для "розового" шума с уровнями звукового давления в n октавах Lокт будет справедливо:
L = Lокт + 10 lg n
Поскольку обычно во внимание принимается 9 октав ( с 31,5 по 8000 Гц), то
L = Lокт +10 lg 9 = Lокт + 9,5 ,дБ
Следует отметить еще одну интегральную характеристику шумов, учиты-вающую различную чувствительность человеческого уха к разным частотным диапазонам. Как известно, ухо человека субъективно занижает низкочастотные звуки и несколько завышает высокочастотные. В связи с этим, вводится поня-тие корректированного уровня звука LА,дБА. Он определяется путем введения специальных корректирующих поправок δ в уровни звукового давления Li ка-ждой октавной полосы с последующим энергетическим суммированием во всем частотном диапазоне:
| n | 0 ,1( Li +δ | |||||
| LА = 10 lg ∑10 | i | ) | ,дБА | (1.47) | ||
i =1
Значения корректирующих поправок приведены в таблице 5.
Таблица 5.
Корректирующие поправки δ i
| Среднегеометрическая | ||||||||||
| частота октавных | 31.5 | 1 000 | 2 000 | 4 000 | ||||||
| полос, Гц | ||||||||||
| Корректирующая | -32,0 | -26,0 | -16,1 | -8,6 | -3,2 | 0,0 | +1,2 | +1,0 | -1,1 | |
| поправка δi дБ | ||||||||||
Очевидно, что значение корректированного по шкале А уровня звука LА будет несколько выше L, если в спектре будут присутствовать высокочастот-ные составляющие и меньше L - для низкочастотного звука. В случае, когда разница между уровнями LА и L будет достигать - 10 дБ…- 20 дБ, можно го-ворить о присутствии инфразвуковых колебаний.
Корректирующая поправка при проведении измерении уровней шума вносится автоматически с помощью специальных корректирующих фильтров, встроенных в прибор. При проведении акустических расчетов эта поправка вносится по формуле (1.47).
Дата добавления: 2016-01-03; просмотров: 2436;
