Отражение звука от препятствий и на границе двух сред
Как во всяком волновом процессе, при падении звуковых волн на препят-ствие ограниченных размеров помимо интерференции наблюдается их отраже-ние (рис.1.10). При этом углы падения и отражения равны друг другу. Следова-тельно, плоские и выпуклые поверхности рассеивают звук (рис.1.10 а, б и в.), а вогнутые – фокусируя, концентрируют его в некоторой точке (рис.1.10 г) .
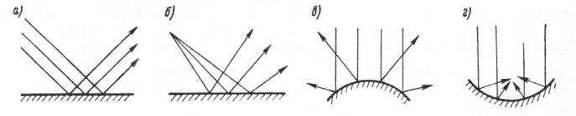
Рис.1.10 Отражение звуковых волн от поверхностей различной формы
При падении волн на границу двух сред (рис.1.11) часть звуковой энергии отражается, а часть проходит во вторую среду.
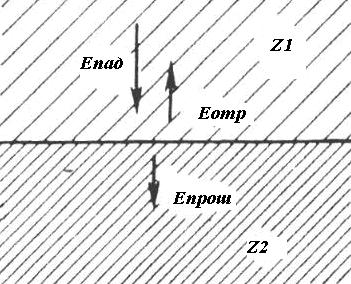
Рис. 1.11 Отражение и прохождение волн на границе двух сред
Согласно закону сохранения энергии сумма прошедшей Епрош. и отражен-ной Еотр. энергий равна энергии падающей волны Епад,, т.е.
| Епад = Еотр. + Епрош. | (1.59) |
Разделим правую и левую части формулы на Епад.
1 = (Еотр./ Епад) +( Епрош/ Епад)
Слагаемые в вышеприведенном соотношении показывают, какая доля па-дающей энергии отразилась, и какая доля прошла дальше. Они представляют собой коэффициенты отражения и прохождения. Вводя для них обозначения η и τ соответственно, получим
| η + τ = 1 | (1.61) | |
| При нормальном падении звуковых волн на границу двух сред с акусти- | ||
| ческими сопротивлениями Z1 и Z2 справедливы следующие выражения | ||
| η = (Z1 – Z2 )2 / (Z1 + Z2 )2 = (1 – Z2 / Z1 )2 / (1+ Z2 | / Z1 )2 | (1.62) |
| τ = 1 – υ = 1 – (Z1 – Z2 )2 / (Z1 + Z2 )2 = 4 Z1 Z2 / (Z1 | + Z2) | (1.63) |
На рис.1.12 показано изменение коэффициентов отражения и прохожде-ния в зависимости от соотношения акустических сопротивлений граничащих сред. Из графика видно, что величина коэффициентов зависит только от абсо-
лютного значения отношений акустических сопротивлений сред, но не зависит от того, какое из этих сопротивлений больше. Этим можно объяснить тот факт, что звук, распространяющийся в какой-либо массивной стенке, претерпевает такое же отражение от границы раздела с воздушной средой, что и звук, рас-пространяющийся в воздухе, при отражении от этой стены.
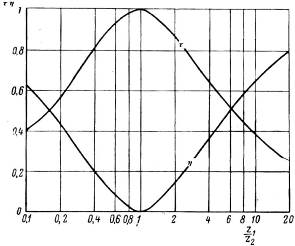
Рис. 1.12. Коэффициенты η и τ в зависимости от соотношения акустических сопротивлей граничаших сред (Z1/Z2)
В ряде случаев представляет интерес знать, как изменится звуковое дав-ление или колебательная скорость частиц при прохождении через границу двух сред. Поскольку интенсивность звуковой энергии пропорциональна квадратам звукового давления и виброскорости, то очевидно коэффициент отражения для давления и скорости можно найти по формуле
| ′ | I | отр | Z | − Z2 | ||||||||||
| η | = Iпад . | = | Z | + Z2 | (1.64) | |||||||||
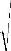
Для коэффициента прохождения по давлению и виброскорости получим
| τ′ = 2 Z2 / (Z1 + Z2) | (1.65) |
Вышеприведенные формулы для коэффициентов отражения и прохождения можно использовать в расчетах одномерных звуководов при изменении их се-чения (рис.1.13), если площади сечения S1 и S2 не слишком отличаются. При
| ствие Епрош. |
поперечных размерах звуковода малых по сравнению с длиной волны (b << λ), акустическое сопротивление его отдельных участков определится произведе-нием площади сечения S и акустического сопротивления среды, заполняющей звуковод (Z1= ρс S1и Z1= ρс S1). Тогда
| η = (S1 – S2 )2 / (S1 + S2 )2 = (1 – S2 / S1 )2 / (1+ S2 / S1 )2 | (1.66) |
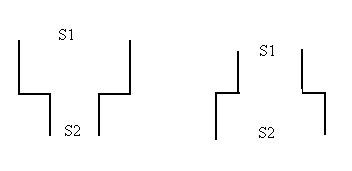
Рис.1.13. Изменение сечений звуковода
Звукопоглощение
Поглощение звука (демпфирование, диссипация) — превращение звуко-вой энергии в тепло. Оно вызывается как теплопроводностью и вязкостью (классическое поглощение), так и внутримолекулярным отражением. При очень больших амплитудах, которые встречаются лишь вблизи очень мощных источ-ников звука или при сверхзвуковом ударе, возникают нелинейные процессы, приводящие к искажению формы волны и к усиленному поглощению.
Для звука в газах и жидкостях поглощение имеет практически важное значение только тогда, когда звук распространяется на большие расстояния (как минимум несколько сотен значений длины волны) или если на пути звука встречаются тела с очень большой поверхностью.
Рассмотрим процесс прохождения звука через препятствие (рис.1.14). Энергия падающего звука Епад. разделяется на энергию отраженную от пре-пятствия Еотр, поглощенную в нем Епогл и энергию прошедшую через препят-
Согласно закону сохранения энергии
| Епад = Еотр. + Епогл + Епрош. | (1.66) |
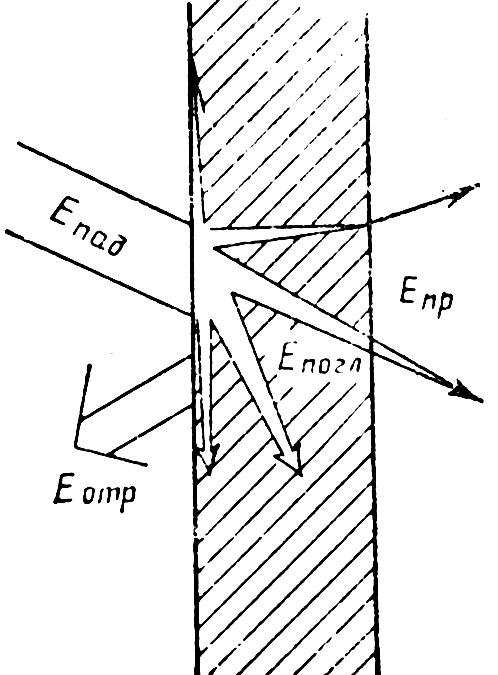
Рис.1.14. Распределение энергии при падении звука на препятствие.
Этот процесс можно оценить отношениями энергий прошедшей, погло-щенной и отраженной к энергии, падающей на препятствие:
τ = Епрош. / Епад ; η = Еотр. / Епад ; α = Епогл. / Епад; (1.67)
Как уже было сказано выше, первые два отношения называют коэффици-ентами прохождения τ и отражения η. Третий коэффициент характеризует долю поглощенной энергии и называется коэффициентом поглощения α. Оче-видно, что из (1.66) следует
| α + η + τ = 1 | (1.68) |
Поглощение звука обусловлено переходом колебательной энергии в теп-ло вследствие потерь на трение в материале. Потери на трение велики в порис-тых и рыхлых волокнистых материалах. Конструкции из таких материалов уменьшают интенсивность отраженных от поверхности звуковых волн. Звуко-поглотители, расположенные внутри помещения, могут уменьшать также ин-тенсивность прямого звука, если они располагаются на пути распространения звуковых волн.
Резонаторы.
Эффективным поглотителем звуковых волн, а в некоторых случаях их усилителем может служить так называемый резонатор. Под резонатором пони-
мается система типа "масса-пружина", в которой роль колеблющейся массы играет масса воздуха в узком отверстии или в щели пластины, а роль пружины
– упругий объем воздуха в полости за пластиной. Схематическое изображение резонатора Гельмгольца приведено на рис.1.15
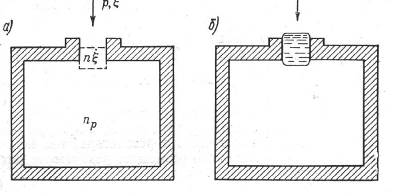
Рис. 1.15. Резонатор Гельмгольца
Рассмотрим простейший воздушный резонатор, т.е. сосуд с жесткими стенками и узким горлом. При падении на него звуковой волны определенной частоты воздушная "пробка" в горле сосуда приходит в интенсивное колеба-тельное движение. Колебательная скорость частиц в горле в несколько раз пре-вышает колебательную скорость в свободном звуковом поле ξ . Во внутреннем объеме резонатора в это время соответственно увеличивается давление р. Если подвести к внутренней полости резонатора трубку, то воспринимаемый звук будет громче.
В тоже время, при достаточно больших потерях на трение резонатор мо-жет выполнять функции не усилителя, а поглотителя звуковой энергии. Если в горло резонатора ввести слой звукопоглощающего материала, то поглощение заметно возрастет.
Собственная круговая частота ωо с массой m на пружине с жесткостью s можно найти по известной формуле
| ω0 = 2π ⋅ f0 = | s / m | (1.69) |
Жесткость пружины определяется в зависимости от площади S попереч-ного сечения горлышка резонатора и объема его полости V по формуле
s = ρо со2 S 2 / V (1.70)
Масса m включает в себя массу воздуха mh в горлышке резонатора глу-биной l и колеблющуюся вместе с ней присоединенную массу окружающего воздуха mm
| m = mh + mm = ρо S l + ρо( | li + lα ), | (1.71) |
| здесь поправочные элементы Δli и Δlα | представляют собой концевые по- |
правки , величина которых зависит от формы горлышка и площади его попе-речного сечения. Таким образом, собственная частота резонатора определится как
| fo = | со | S | (1.72) | ||||
| 2π | V (l + li + lα ) | ||||||
В таких резонансных системах в присутствии внешнего источника звука заключенный в полости воздух колеблется с ним в унисон с амплитудой, зави-сящей от соотношения между величинами периодов собственного и вынужден-ного колебаний. При отключении источника резонатор отдает назад накоплен-ные внутри него колебания, становясь на короткое время вторичным источни-ком.
В зависимости от характеристик, резонатор может либо усиливать, либо поглощать звуковые колебания на той или иной частоте.
Звукопоглощение резонатора описывается с помощью условной характе-ристики звукопоглощающего сечения А. Под ним понимается условная пло-щадь сечения, перпендикулярного направлению распространения падающей волны, через которую свободной волной (при отсутствии резонатора) передает-ся мощность, равная поглощаемой резонатором.
Положим, что размеры резонатора малы по сравнению с длиной падаю-щей волны. Тогда, в первом приближении, можно пренебречь рассеянием зву-ковой энергии на корпусе резонатора. Если принять отверстие резонатора за-крытым акустически жестко, то звуковое давление в горлышке ph= pl , а ко-лебательная скорость υ = ph/ Zh (если резонатор находится на экране, то в приведенных формулах добавится множитель 2).
Импеданс горлышка резонатора складывается из внутреннего потерь Ri, активного сопротивления излучения Rr и реактивных сопротивлений массы и упругости.
| Zh = Ri + Rr + ( jωm + s /jω) / S | (1.73) |
здесь реактивное сопротивление излучения уже учтено в поправочном элемен-те Δl при определении т.
Потери звуковой энергии в резонаторе могут быть определены как
| Ph = υh2 R i S = pl2 S R i / 2 Zh2 | (1.74) |
| Отсюда звукопоглощающее сечение определится из выражения | |
| А = 2 Ph / (pl2 /Zo) = S R i Zo / Zh2 | (1.75) |
| здесь Zo - величина импеданса на резонансной частоте fo , при этом | мнимые |
| части из всех выражений исчезают и тогда | |
| А = S R i Zo / (R i + R l) | (1.76) |
2 . П Р О М Ы Ш Л Е Н Н А Я А К У С Т И К А
Дата добавления: 2016-01-03; просмотров: 2477;
