Адсорбция на границе твердое тело-газ

Адсорбция увеличивается с ростом давления газа, однако это увеличение не беспредельно. Кривая зависимости адсорбции от давления при постоянной температуре носит название изотермы адсорбции. Она является одной из важнейших характеристик адсорбционных процессов. Как видно из рисунка, повышение давления газа увеличивает адсорбируемое количество его.

Однако на разных участках изотермы это влияние сказывается по-разному. Наиболее сильным оно оказывается в области низких давлений I, где адсорбция прямопропорциональна давлению газа. Дальнейшее повышение давления сопровождается увеличение количества адсорбента, но уже в меньшей степени (область II). При достаточно высоких давлениях (область III) изотерма стремится к прямой, параллельной оси абсцисс.

Математическая зависимость количества адсорбируемого вещества от давления выражается уравнением Фрейндлиха:

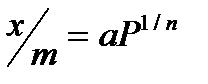, (3)

где x – количество адсорбированного газа; m – количество поглотителя; P - равновесное давление газа над поглотителем; а и n – константы, характерные для данного процесса.

Для определения констант а и n уравнение Фрейндлиха логарифмируют: 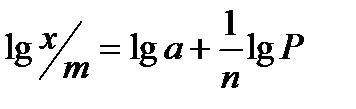. (4)

График в координатах 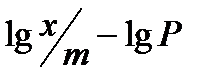имеет вид прямой, которая отсекает на оси ординат отрезок, равный lg a, а тангенс угла наклона этой прямой к абсциссе дает значение 1/n.

Уравнение Фрейндлиха имеет следующие ограничения:

1. Константы a и n являются эмпирическими и не имеют физического смысла.

2. Данное уравнение применимо только для области средних давлений.

Позднее (1917 г.) Ленгмюр вывел уравнение адсорбции с допущением, что все места на поверхности твердого тела энергетически равноценны и между частицами отсутствует взаимодействие, т.е. при адсорбции отсутствует диссоциация или ассоциация. Уравнение изотермы адсорбции тогда принимает следующий вид:

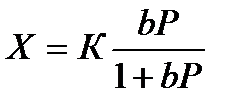. (5)

где b – адсорбционный коэффициент, равный отношению констант скорости адсорбции k1 и десорбции k2.

Анализ уравнения Ленгмюра:

1. При слабой адсорбции (b мало) и при низком парциальном давлении пара адсорбирующего вещества (Р мало) можно считать 1+bP≈1, тогда уравнение (3) принимает следующий вид: x = KbP. Следовательно, при этих условиях степень заполнения поверхности прямопропорциональна парциальному давлению вещества.

2. Для области высоких давлений значения b и Р велики и 1+bP≈bP, т.е. уравнение (3) принимает вид: x = K. Поверхность твердого тела при высоких давлениях полностью заполнена адсорбтивом и дальнейшее увеличение парциального давления вещества в газовой смеси не влияет на количество адсорбированного вещества на поверхности тв. тела.

Установлено, что уравнение Ленгмюра хорошо применимо для областей низких и высоких давлений и все величины, входящие в данное уравнение, имеют определенный физический смысл и обоснованы теоретически.