Теорема умножения вероятностей. Теорема. Вероятность совместного наступления двух событий (АВ) равна произведению вероятности одного из этих событий на условную вероятность второго
Теорема. Вероятность совместного наступления двух событий (АВ) равна произведению вероятности одного из этих событий на условную вероятность второго, вычисленную в предположении, что первое событие наступило, т.е. 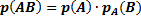 .
.
Доказательство. Пусть наступлению события А благоприятствуют 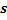 исходов из
исходов из 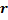 равновозможных, не совместных и единственно возможных. Тогда безусловная вероятность события А будет равна
равновозможных, не совместных и единственно возможных. Тогда безусловная вероятность события А будет равна
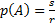 .
.
Пусть далее из 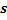 исходов, при которых наступает событие А, наступлению события В благоприятствуют
исходов, при которых наступает событие А, наступлению события В благоприятствуют 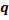 исходов (
исходов ( 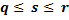 ). Тогда условная вероятность события В, вычисленная в предположении, что произошло событие А, будет равна
). Тогда условная вероятность события В, вычисленная в предположении, что произошло событие А, будет равна
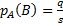 .
.
Вычислим теперь вероятность наступления событий и А, и В. Совместное наступление событий и А, и В может иметь место только в 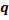 случаях из
случаях из 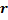 равновозможных. Следовательно,
равновозможных. Следовательно,
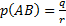 .
.
Разделив и умножив эту дробь на 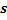 , получим
, получим
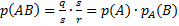 .
.
Заметим, что 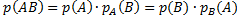 .
.
Вероятность совместного наступления нескольких взаимозависимых событий (АВС…LК) равна произведению вероятности первого события на условную вероятность второго в предположении, что первое наступило, на условную вероятность третьего в предположении, что первые два наступили, и т.д., т.е.
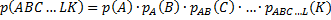
Теорема. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий, т.е. 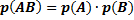 .
.
Доказательство. Из доказанной теоремы следует 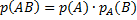 . Так как события А и В независимы, то
. Так как события А и В независимы, то 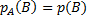 . Следовательно,
. Следовательно, 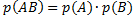 .
.
Вероятность совместного появления нескольких независимых событий А, В, С,…,К равна произведению вероятностей этих событий, т.е.
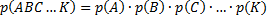 .
.
Дата добавления: 2015-12-29; просмотров: 775;
