Векторного умножения векторов

А1⁰. .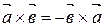

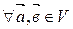А2⁰. .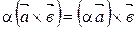

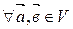
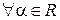А3⁰. .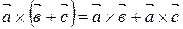

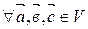Замечание. Пользуясь определениями ортонормированного базиса и векторного произведения двух векторов, можно доказать, что

;	;	;
;	;	;
;	;	.

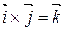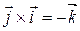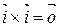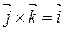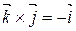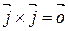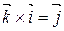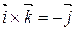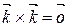Попробуйте доказать самостоятельно!

Теорема 1 (векторное произведение в координатах). Если 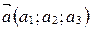, 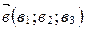в базисе 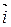, , 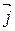, 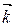то

.

По определению координат вектора в базисе , ,

, .

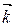
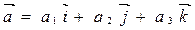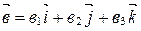Тогда 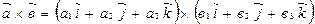. Используя свойства А1⁰-А3⁰ векторного умножения и замечание, получим:

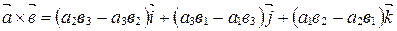
(получите это равенство, проделав все выкладки самостоятельно).

Применение векторного произведения

Векторное произведение двух векторов применяется:

1. Для выяснения коллинеарности двух векторов: || .

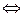
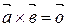2. Для вычисления площади параллелограмма: 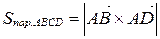(рис. 21).

3. Для вычисления площади треугольника: .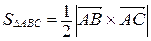

Задания для самостоятельной работы

1. Изобразите на чертеже векторы 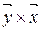; 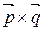(рис. 23).

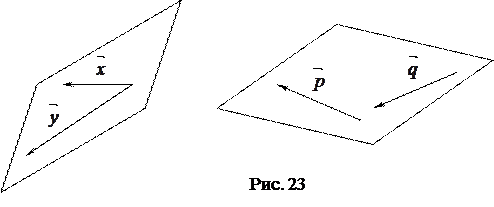2. Примените алгебраические свойства векторного умножения для упрощения выражения .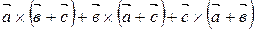

3. Пользуясь определением векторного произведения, докажите, что векторы 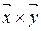и 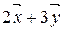ортогональны.

4. Вычислите: .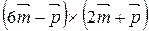

5. Вычислите площадь 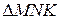, если , .

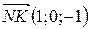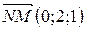Лекция 6

Нелинейные операции над векторами