Смешанного умножения векторов. А10. Циклическая перестановка сомножителей не меняет смешанного произведения, т.е
А10. Циклическая перестановка сомножителей не меняет смешанного произведения, т.е. 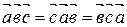
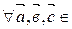 V.
V.
Перестановка двух соседних сомножителей меняет знак смешанного произведения на противоположный, т.е.
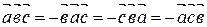 ,
, 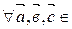 V.
V.
Для доказательства достаточно применить доказательство свойства Г20 к 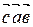 и к
и к 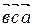 . Параллелепипед будет тот же, только за основание будет принята другая грань (в первом случае – построенная на векторах
. Параллелепипед будет тот же, только за основание будет принята другая грань (в первом случае – построенная на векторах 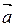 и
и 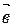 , во втором – на векторах
, во втором – на векторах 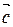 и
и 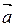 ).
).
Чтобы доказать вторую часть свойства, надо воспользоваться определением смешанного произведения и свойством А10 векторного умножения, а затем совершить циклическую перестановку:
 .
.
А20. 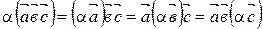
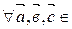 V
V 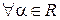 .
.
Для доказательства этого свойства нужно доказать три равенства:
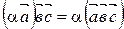 ;
; 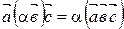 ;
; 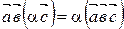 .
.
Докажите их самостоятельно, пользуясь определением смешанного произведения и алгебраическими свойствами скалярного и векторного умножения векторов.
А30. 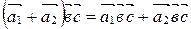 ;
;
 ;
;
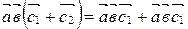 .
.
Докажите эти равенства самостоятельно, пользуясь определением смешанного произведения и алгебраическими свойствами скалярного и векторного умножения векторов.
Замечание. Смешанное произведение  .
.


 , т.к.
, т.к. 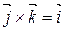 .
.
Теорема 1(смешанное произведение в координатах). Если 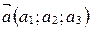 ,
, 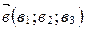 ,
, 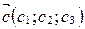 в базисе
в базисе 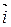 ,
, 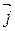 ,
, 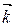 , то
, то 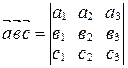 .
.


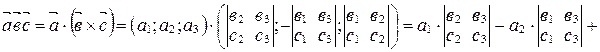
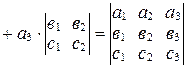 .
.
Дата добавления: 2015-11-28; просмотров: 1463;
