Основная метрическая задача

Теорема 3(расстояние между двумя точками в координатах). Если в прямоугольной декартовой системе координат 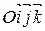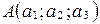, , 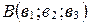то расстояние АВ между точками А и В находится по формуле:

.

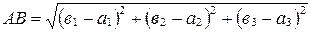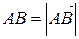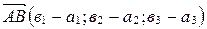Учитывая, что , и используя формулы для нахождения длины вектора в координатах, получаем:

.

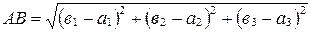Формулы, доказанные в теоремах 1 и 2, можно использовать и в аффинной, и в прямоугольной декартовой системе координат, а формулу из теоремы 3 – только в прямоугольной декартовой системе координат.

Задания для самостоятельной работы

1. Найдите координаты точки А, если В(3;0;-2), .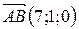

2. С – середина отрезка АВ. Найдите координаты точки В, если А(1;0;-4), С(3;1;0).

3. Точки Р и Q лежат внутри отрезка АВ, причем АР=РQ=QВ. Найдите (ВQ,А).

4. На плоскости дан отрезок [АВ]. Постройте точку С, делящую направленный отрезок 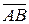в отношении ; .

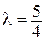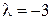5. Известны координаты вершин треугольника АВС: А(4;3), В(0;5),С(-2;2). Пользуясь теоремой, обратной теореме Пифагора, выясните, будет ли этот треугольник прямоугольным.

6. Можно ли вывести формулы для нахождения расстояния между двумя точками, координаты которых даны в аффинной системе координат?

Лекция 8