Частные случаи преобразования аффинной

Системы координат

1. Перенос начала.

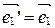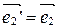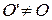При этом преобразовании , , а (рис. 40).

Найдем координаты векторов 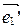и 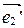в старой системе, т.е. 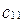, , 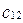и :

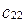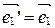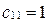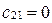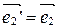Þ Þ , ;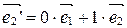

Þ Þ , .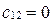

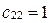Тогда формулы (5) примут вид:

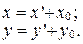
Формулы (6) называются формулами переноса начала.

2. Замена координатных векторов.

При этом преобразовании системы координат имеют общее начало и отличаются координатными векторами (рис. 41).

Так как 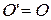, то 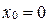, 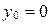. Тогда формулы (5) примут вид:

; .

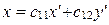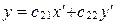Формулы (7) называются формулами замены координатных векторов.

Задания для самостоятельной работы

1. Напишите формулы преобразования аффинной системы координат 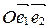в аффинную систему координат 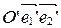, если 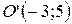, , 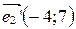в системе .

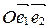2. Может ли матрица перехода от базиса 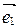, 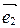к базису 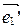, 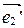иметь вид 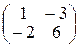и почему?

3. Напишите формулы переноса начала, если 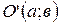в системе координат .

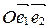4. Напишите формулы замены координатных векторов, если , .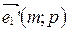

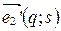5. Запишите матрицу перехода от базиса 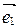, 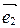к базису 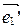, 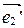в случае:

а) переноса начала;

б) замены координатных векторов.

Понятие направленного угла между векторами.