Возможны различные случаи геометрического расположения поверхностей обратных скоростей и волновых векторов.
Допустим, что перпендикуляр на границу раздела, проходящий через концы векторов обратной скорости, не пересекает одну из поверхностей обратных скоростей. Это означает, что амплитуда этой волны быстро убывает. Аналитически это выражается мнимым решением дисперсионного уравнения для прошедшей волны
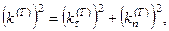
при этом критический угол падения 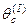 , при котором
, при котором 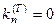 и
и 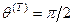 определяется соотношением
определяется соотношением 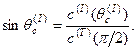
Падениеволны поперечной поляризации с вектором поляризации,
перпендикулярным плоскости падения.
Выберем оси координат так, что плоскость падения соответствует плоскости 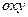 , а граница раздела плоскости
, а граница раздела плоскости 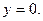 При таком выборе осей координат нормаль к границе раздела соответствует орту оси
При таком выборе осей координат нормаль к границе раздела соответствует орту оси 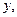 а единственным отличным от нуля перемещением будет перемещение по оси
а единственным отличным от нуля перемещением будет перемещение по оси  Пусть
Пусть  волновое число падающей волны,
волновое число падающей волны, 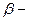 угол падения,
угол падения, 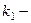 волновое число отраженной волны,
волновое число отраженной волны, 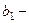 скорость поперечных волн в упругой среде падающей волны,
скорость поперечных волн в упругой среде падающей волны, 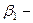 угол отражения,
угол отражения, 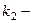 волновое число преломленной волны,
волновое число преломленной волны, 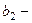 скорость поперечных волн в упругой среде, куда преломляются волны,
скорость поперечных волн в упругой среде, куда преломляются волны,  угол преломления,
угол преломления, 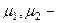 модули сдвига упругих сред. Таким образом, решение можно искать в виде:
модули сдвига упругих сред. Таким образом, решение можно искать в виде:
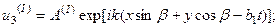
 (4.7.8)
(4.7.8)
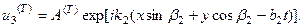
Дата добавления: 2015-12-29; просмотров: 879;
