Учитывая, что получим
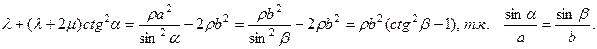
Тогда компоненты напряжений 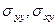 на границе раздела сред можно переписать в виде:
на границе раздела сред можно переписать в виде:
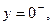
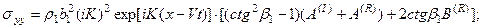
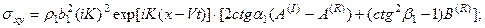
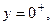
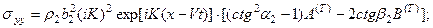
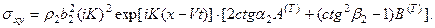
Равенство перемещений и компонент вектора напряжений на границе раздела приводит к следующей системе уравнений:
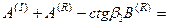
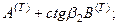
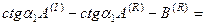
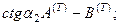
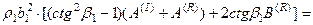
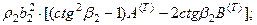

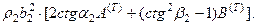
Для упрощения записи введем в качестве новых неизвестных отношение амплитуд отраженных и преломленных волн к амплитуде падающей волны:
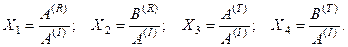
Тогда граничные приводят к системе уравнений :
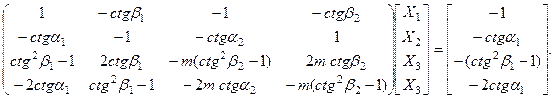
Полученная система уравнений позволяет найти амплитуды отраженных и преломленных волн численно. Поскольку аналитические вычисления в общем случае громоздки, рассмотрим предельные случаи падения волны на жесткую стенку и на свободную поверхность. В первом случае достаточно приравнять к нулю перемещения на границе при  Система уравнений при этом примет вид:
Система уравнений при этом примет вид:
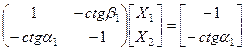 ,
,
А ее решения будут иметь вид
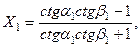
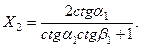
Интересно отметить, что в предельном сучае, когда , получим Это означает, что при нормальном падении продольной волны, поперечная волна не отражается, а отраженная продольная волна имеет амплитуду, равную амплитуде падающей волны.
Можно задать вопрос: возможна ли реализация такого отражения, при котором отражается только поперечная волна, а амплитуда продольной отраженной волны равна нулю? Это означает равенство нулю выражения 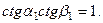 Учитывая, что углы отражения связаны со скоростями волн соотношением
Учитывая, что углы отражения связаны со скоростями волн соотношением 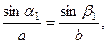 получим уравнение для определения
получим уравнение для определения 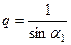 :
:
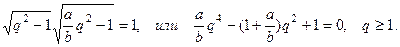
Приведенное квадратное уравнение 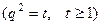
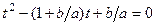
Имеет корни , лишь один из которых является подходящим по физическому смыслу, но он соответствует предельному случаю , в котором волна не падает, а распространяется параллельно стенке. Вывод однозначен – при всех углах падения отражаются как продольная, так и поперечная волны.
Рассмотрим случай падения продольной волны на свободную поверхность. В этом случае на границе должны быть равны нулю компоненты вектора напряжений 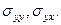 Это приводит к системе уравнений:
Это приводит к системе уравнений: 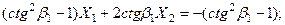

Решение которой дают выражения:
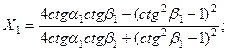
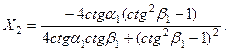
В предельном случае нормального падения продольной волны ( 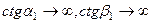 ) получим ожидаемый результат
) получим ожидаемый результат 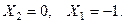
Дата добавления: 2015-12-29; просмотров: 748;
