Из условий (4.7.2) следует, что в любой момент времени

(4.7.3)

Следовательно, при отражении и преломлении волн их частота не меняется. Кроме того, в любой точке плоскости 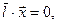должны выполняться условия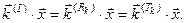

Эти условия можно переписать в форме:

(4.7.4)

Из сравнения уравнения (4.7.4) с уравнением плоскости следует, что векторы должны быть перпендикулярны самой плоскости раздела сред, т.е. параллельны вектору

Отсюда следуют два общих свойства:

1). Волновые векторы отраженных и преломленных волн всегда расположены в плоскости, определяемой вектором падающей волны и вектором нормали к поверхности раздела;

2). Проекции всех волновых векторов на поверхность раздела одинаковы, т.е. (4.7.5)

где угол падения и углы отражения и преломления (рис.4.1).

Поскольку частоты всех волн равны между собой, а фазовая скорость волновое число и частота связаны соотношением отсюда следует закон отражения – преломления

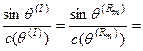
(4.7.6)

Для изотропной среды он будет иметь более простой вид:

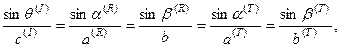(4.7.7)

где углы отражения продольных и поперечных волн, углы преломления продольных и поперечных волн.

Рис.4.1 Волновые векторы падающей, отраженных и преломленных волн.

Удобными для анализа отражения и преломления волн являются поверхности обратных скоростей. Для примера на рис.4.2 приведены поверхности обратных скоростей для кубического кристалла кремния, граничащего с изотропной средой – плавленым кварцем. Падающая квазипродольная волна порождает отраженные квазипродольную и квазипоперечную отраженные волны, а также продольную и поперечную преломленные волны в изотропной среде, отраженная волна с поляризацией, перпендикулярной плоскости падения не отражается, так как смещение падающей волны не содержит компоненты вдоль этого направления.

Построение поверхностей обратных скоростей позволяет также определить скорости переноса энергии для каждой из волн, поскольку вектор скорости переноса энергии перпендикулярен поверхности обратных скоростей.

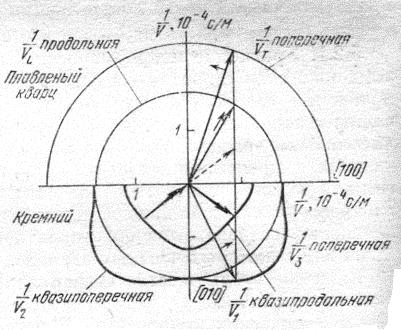
Рис.4.2 Геометрическое построение волновых векторов для отраженных и преломленных волн на границе кремний – плавленый кварц.