IV. Электромагнитный момент
Электромагнитная мощность равна произведению электромагнитного вращающего момента 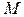 и угловой скорости вращения
и угловой скорости вращения 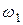 магнитного потока
магнитного потока
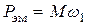 .
.
Механическая мощность на валу ротора равна произведению момента 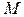 на угловую скорость вращения
на угловую скорость вращения 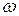 ротора
ротора
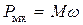 .
.
Разность электромагнитной и механической мощностей, затрачиваемая на электрические потери в активном сопротивлении ротора,
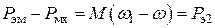 .
.
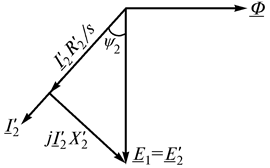 Рис. 11.9
Рис. 11.9
|
Учитывая (11.31), получим
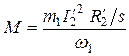 ,
,
где 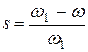 .
.
Из векторной диаграммы для ротора (рис. 11.9) получаем
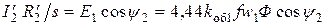 .
.
Формула для вращающего момента приобретает вид
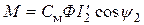 , (11.42)
, (11.42)
где 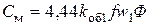 – постоянный коэффициент.
– постоянный коэффициент.
Из (11.42) следует, что вращающий момент пропорционален произведению магнитного потока и активной составляющей тока ротора. Для определения момента через параметры двигателя выразим ток 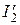 из схемы рис. 11.6 в без учета тока холостого хода
из схемы рис. 11.6 в без учета тока холостого хода
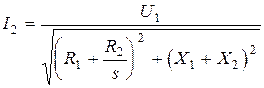
и 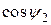 через параметры ротора
через параметры ротора
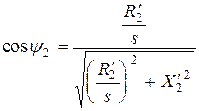 .
.
Подставив последнее соотношение в (11.42) с учетом
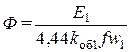 ,
, 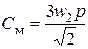 ,
,
где 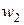 – число витков ротора на одну фазу статора (число фаз
– число витков ротора на одну фазу статора (число фаз 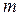 = 3); р – число пар полюсов;
= 3); р – число пар полюсов; 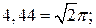
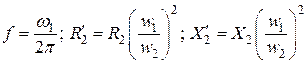 , получаем
, получаем
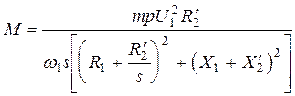 . (11.43)
. (11.43)
Согласно (11.43) электромагнитный момент при любом скольжении пропорционален квадрату напряжения фазы статора и тем меньше, чем больше 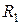 и индуктивное сопротивление машины
и индуктивное сопротивление машины 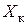 .
.
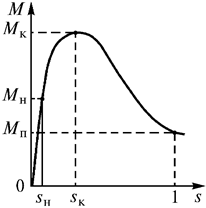 Рис. 11.10
Рис. 11.10
|
Графическая зависимость 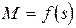 показана на рис. 11.10.
показана на рис. 11.10.
Характерными точками для режима двигателя являются:
режим холостого хода: 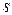 = 0,
= 0, 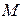 = 0;
= 0;
номинальный режим: 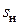 =0,02…0,06,
=0,02…0,06, 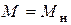 ;
;
режим максимального (критического) момента: 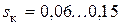 ,
, 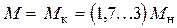 ;
;
режим пуска: 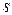 = 1,0,
= 1,0, 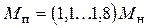 .
.
Максимум вращающего момента разделяет кривую на устойчивую часть от 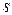 = 0 до
= 0 до 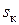 и неустойчивую – от
и неустойчивую – от 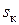 до
до 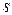 = 1. Увеличение тормозного момента выше максимального ведет к остановке двигателя.
= 1. Увеличение тормозного момента выше максимального ведет к остановке двигателя.
Максимальный момент и критическое скольжение можно выразить через параметры машины, приравняв к нулю первую производную 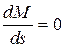 по (11.43)
по (11.43)
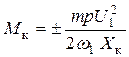 , (11.44)
, (11.44)
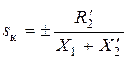 . (11.45)
. (11.45)
В этих соотношениях знак плюс относится к двигательному, знак минус – к генераторному режиму работы. Напомним, что формулы получены без учета активного сопротивления обмотки статора.
Путем преобразования уравнения (11.43) с учетом (11.44) и (11.45) получим формулу момента в относительных единицах
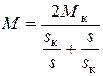 .
.
Дата добавления: 2015-12-16; просмотров: 2124;
