Волны поперечной поляризации, имеющие скорость
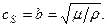(4.4.5)
Поскольку за счет выбора осей можно искать решение в виде:
- 
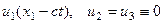для продольных волн;
- 
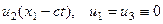для поперечных волн.
Продольная волна: волновой вектор и поляризация волны параллельны. Частицы колеблются вдоль одной прямой. В заданный момент времени волна представляет собой последовательность областей сжатия и разрежения.
Поперечная волна: поляризация и волновой вектор перпендикулярны. Частицы отклоняются в обе стороны от прямой, на которой они находятся в отсутствие волны. Плоскости, перпендикулярные волновому вектору, скользят одна относительно другой, причем расстояния между ними не меняются.
Следовательно: на фронте продольных волны изменяется объем, а на фронте поперечных волн изменяется форма при сохранении объема.
Рассмотрим волны произвольной геометрии фронта. Для этого воспользуемся представлением векторного поля в виде суммы двух полей. При этом мы существенно пользуемся линейностью уравнений.
Любое непрерывное, ограниченное в области векторное поле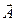 
можно представить в виде суммы потенциального и соленоидального полей
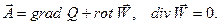(4.4.6)
Действительно, применяя к (4.4.1) сначала операциюdiv , а затем – rot, для определения функции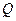 
и вектор-функции 
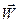получим уравнения Пуассона:
Дата добавления: 2015-12-29; просмотров: 788;