Связь между сдвиговым напряжением и сдвиговой деформацией можно получить из решения задачи чистого сдвига.

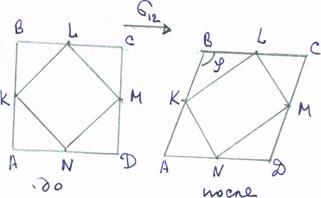
Пусть в недеформированном состоянии образец представлял собой куб со стороной2l.При чистом сдвиге квадрат в основании куба превращается в ромб, а квадратKLMNпревращается в прямоугольник. СтороныKL,NMудлиняются, а стороныKN,LMукорачиваются. 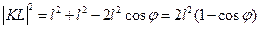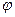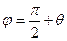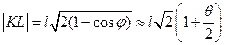Начальная длинаKL=l√2,а текущая определяется по теореме косинусов для треугольникаBKL: , где угол представляет собой измененный за счет малой деформации первоначально прямой угол - , причем |θ|<<1, тогда , а деформация 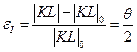(4.2.2)

Определим, какое напряжение вызвало удлинение элементаKL. Напряженное состояние при чистом сдвиге, представленном на рисунке, описывается тензором, у которого только . Вектор напряжений на площадкеLM, имеющей нормаль будет равен . Аналогично на площадкеKLс нормалью получится .

Итак, в системе координат с репером 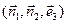напряженное состояние представляет собой растяжение вдоль оси 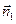напряжением 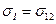и сжатие по оси 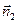напряжением 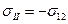. Напряжение вдоль третьей оси равно нулю 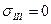. Воспользуемся формулами (4.2.1), (4.2.2) и вспомним геометрический смысл смешанных компонент тензора деформаций:

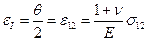(4.2.3)

Выражения (4.2.1) и (4.2.3) можно объединить для произвольного деформационного состояния 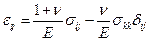(4.2.4)

Зная (4.1.6), (4.2.4) можно легко получить выраженияλ, μчерезE, ν:

.

Уравнения Ламе.

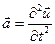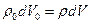
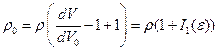Рассматриваем случай малых перемещений и деформаций, тогда, как обсуждалось в первом разделе, Лагранжевы и Эйлеровы координаты совпадают, а в тензоре деформаций можно пренебречь нелинейным членами (1.4.13). Вектор ускорения можно в этом случае взять в Лагранжевой форме , а закон сохранения массы для выделенного элемента сплошной среды записать в виде или , где 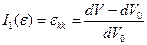- объемная относительная деформация.

Итак, линеаризованную полную систему уравнений, описывающих движение упругой среды в этом случае, можно представить в следующем виде: 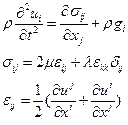(4.3.1)