Обобщенный закон Гука.

Известно, что для многих твердых материалов справедлив закон Гука, устанавливающий линейную зависимость между напряжением и деформацией при одноосном растяжении (сжатии) образца. Т.е., еслиF - сила, с которой растягивается образец начальной длины 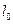и сечения 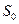, то напряжение -σ=F/S и деформация - 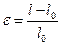связаны зависимостьюσ=Eε, гдеE- модуль Юнга материала образца. Отметим, что для большинства материалов эта зависимость справедлива лишь для малых значений деформации. В общем случае напряженно-деформированного состояния сплошной среды необходимо обобщение закона Гука. Поэтому нашей целью является получение зависимостей между компонентами тензора напряжений и компонентами тензора деформаций для произвольного нагружения образца упругой сплошной среды. Определим более четко само понятие - упругая среда. Упругой средой будем называть такую среду, для которой деформации являются обратимыми. Это означает, что затраченная на деформацию энергия тоже обратима.

Элементарная удельная работа, совершаемая внутренними поверхностными силами равна 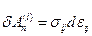(4.1.1)

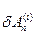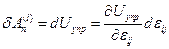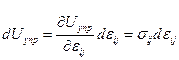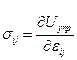Определение. Упругой средой будем называть такую среду, для которой работа внутренних поверхностных сил не зависит от процесса деформирования, а зависит только от начальных и конечных значений компонент тензора деформации. Согласно (4.1.1) это будет означать, что является полным дифференциалом, то есть . Тогда из (4.1.1) и (4.1.2)

Назовем 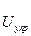- упругой энергией, которая является функцией деформаций 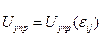. В соответствии с посылом закона Гука напряжения являются функциями деформаций. Мы рассматриваем случай малых деформаций, поэтому величины 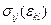можно разложить в ряд Тейлора, а учитывая, что при нулевых деформациях (ε=0)натяжения тоже равны нулю (σ=0), получим: 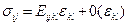(4.1.3)