Энергия упругой деформации. Поток упругой энергии.

Работа, совершаемая внешними силами в процессе деформа­ции, накапливается в теле в виде потенциальной энергии. Как только внешние силы перестают действовать, энергия упругой деформации преобразуется в работу упругих сил, за счет чего тело принимает первоначальную форму. Работа внешних - объемных и поверхностных сил при деформации тела, как было показано, равна

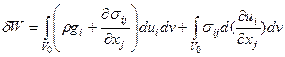
Поскольку выражение, стоящее в скобках в первом интеграле в силу уравнения движения равно 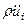, а второй интеграл определяет изменение внутренней упругой энергии (4.1.2), работе можно придать другой вид:

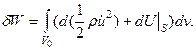
Таким образом, работа затрачивается на изменение полной (кинетической плюс внутренней) энергии среды.

Распространение упругих волн сопровождается переносом энергии. Полная энергия, содержащаяся внутри элементарного объема, увеличивается за счет работы поверхностных сил 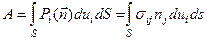, а скорость изменения полной энергии будет определяться выражением: 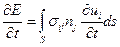. (4.6.1)

Фактически скорость изменения энергии определяется вектором Умова-Пойнтинга 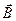, с компонентами 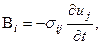(4.6.2)

Направление вектора Умова-Пойнтинга 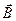является направлением распространения энергии, а его длина равна количеству энергии, переносимому через единицу поверхности, перпендикулярной к направлению распространения энергии, за единицу времени.

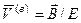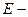Вектор , где полная энергия, называется вектором скорости потока энергии.

Для плоской волны имеем (4.5.2):

- плотность кинетической энергии равна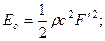

- плотность потенциальной энергии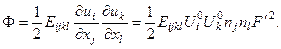

С учетом уравнения (4.5.3), плотность потенциальной энергии можно переписать в форме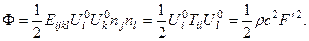

Из полученного выражения следует, что плотность потенциальной упругой энергии и плотность кинетической энергии для плоской волны совпадают по величине. Тогда плотность полной энергии будет равна удвоенной величине любой из них: 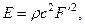а вектор Умова-Пойнтинга: 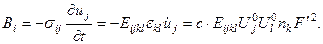В свою очередь для вектора скорости потока энергии: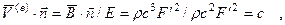

т.е. проекция вектора скорости переноса энергии на нормаль к фронту равна фазовой скорости волны. Отсюда следует, что скорость переноса энергии не меньше фазовой скорости волны.

Для геометрической иллюстрации волновых свойств можно рассмотреть несколько характерных поверхностей:

1).Поверхность, образованная концами вектора 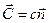называется поверхностью скоростей. Для изотропной среды эта поверхность состоит из двух коаксиальных сфер.

2).Геометрическое место концов вектора 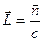называется поверхностью обратных скоростей.

3).Геометрическое место точек, занимаемых концом вектора 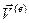для всех направлений распространения волны, называется волновой поверхностью.

Все эти поверхности связаны с распространением волн для данной анизотропной среды. Покажем, что поверхность обратных скоростей позволяет определить направление вектора скорости переноса энергии. Для этого найдем вектор касательный к поверхности обратных скоростей 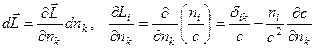. С другой стороны имеем: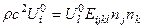

,

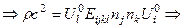
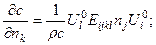
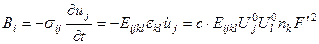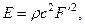
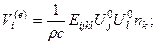
Отсюда следует, что 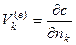, а тогда:

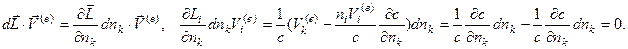
Покажем, что скорость переноса энергии совпадает с групповой скоростью. Поскольку определение фазовой скорости сводится к решению уравнения 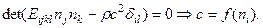Если умножить каждую строку матрицы на 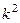и учесть, что 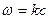, мы получим в точности такую же функциональную зависимость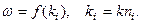

Отсюда следует, что 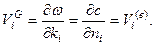Таким образом, групповая скорость совпадает со скоростью переноса энергии.