Из условия (4.7.5) следует, что Из закона отражения – преломления (4.7.7) следует, что
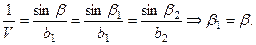
Учитывая это, можно переписать решение (4.7.8) в виде
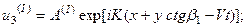
 (4.7.9)
(4.7.9)
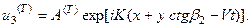
Тогда равенство перемещений при дает уравнение
 (4.7.10)
(4.7.10)
Отличными от нуля компонентами тензора деформаций будут


Соответствующими отличными от нуля компонентами тензора напряжений будут
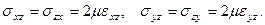
При этом единственной, отличной от нуля, компонентой вектора напряжений на границе раздела будет  Из условия непрерывности вектора напряжений получим:
Из условия непрерывности вектора напряжений получим:
 (4.7.11)
(4.7.11)
Решая систему уравнений относительно амплитуд отраженных и преломленных волн, получим:
 (4.7.12)
(4.7.12)
 (4.7.13)
(4.7.13)
Рассмотрим два предельных случая и . Первый случай соответствует падению волны на жесткую стенку, а второй - падению волны на свободную поверхность. В первом случае получим в результате предельного перехода
 во втором
во втором 
Рассмотрим случай, когда скорость волн во второй среде в два раза больше, чем скорость волн в первой 
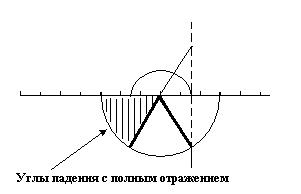
Рис.4.3. При углах больших критического нет регулярного преломления волн.
Падение продольной волны на границу раздела двух сред.
Рассмотрим падение продольной волны на границу раздела двух сред под заданным углом  . Обозначим угол отражения поперечной волны
. Обозначим угол отражения поперечной волны  , а углы преломления продольной и поперечной волн соответственно через
, а углы преломления продольной и поперечной волн соответственно через  . Тогда решение можно искать в виде:
. Тогда решение можно искать в виде:
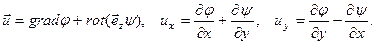
Потенциалы падающей, отраженных и преломленных волн записываются в виде: 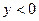
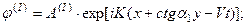
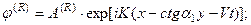


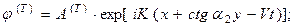
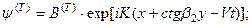
Дата добавления: 2015-12-29; просмотров: 702;
