Подставляя третье уравнение (4.3.1) во второе получим для напряжения

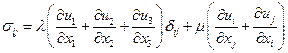, последующая подстановка в первое дает 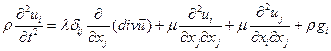или после перегруппировки: 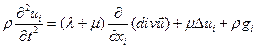(4.3.2)

Полученная система уравнений движения линейно-упругой среды в перемещениях носит имя Ламе. Уравнения Ламе можно записать и векторной форме 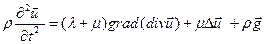(4.3.3)

Используя операторное тождество 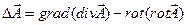, уравнение Ламе можно представить также в виде:

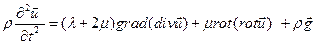(4.3.4)

Упражнение. Выражая перемещения и деформации в системе (4.3.1) через напряжения получить основные уравнения для напряжений (уравнения Бельтрами-Митчелла).

Волны в неограниченной изотропной, линейно-упругой среде.

«Неограниченная» означает, что размеры среды велики по сравнению с размерами волнового пучка, и краевыми эффектами можно пренебречь. Будем искать решение уравнения (4.3.3) в отсутствии массовых сил в виде 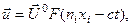(4.4.1)

Где постоянный единичный вектор поляризации волны, произвольная дважды дифференцируемая функция, постоянный единичный вектор. Поскольку уравнение представляет плоскость, движущуюся по нормали со скоростью , такое решение называется плоской волной. С учетом того, что , , подстановка (4.4.1) в (4.3.2) дает

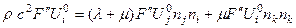. (4.4.2)

После простых преобразований приходим к уравнению , которое после переноса всех членов в одну сторону дает Полученная однородная система уравнений имеет отличное от нуля решение только в том случае, когда ее определитель равен нулю, т.е.

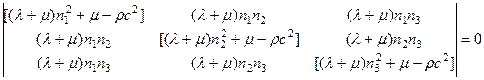. (4.4.3)