Где - коэффициенты разложения. В (4.1.3) мы сохранили только линейную часть разложения, отбросив члены более высокого порядка малости по деформациям.

В разложении (4.1.3) в силу симметрии тензоров напряжений и деформаций . Кроме того, учитывая определение модулей упругости, получим (соотношение Максвелла), откуда следует еще одна симметрия тензора упругих постоянных , т.е. , как следствие равенства смешанных производных энергии по деформациям.

Эти равенства приводят к тому, что в общем случае анизотропной среды из общего числа 81 компонент тензора четвертого рангаE остается всего 21 независимая компонента. Особенно просто получить такой результат, если переобозначить напряжения и деформации в форме , аналогично дляε. Пустьα,β- пробегают значения от 1 до 6, тогда зависимость между напряжениями и деформациями можно записать в виде , где все и - независимы, а независимость закона от нумерации осей приводит к тому, что матрица - симметрична. Отсюда и получаем, что число независимых переменных равно 21.

Определение. Среда, свойства которой по всем направлениям одинаковы, называется изотропной. В случае изотропной среды количество упругих модулей равно 2 и тензор упругих модулей в этом случае имеет вид 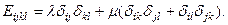. В этом случае упругая энергия должна быть функцией скалярных инвариантов тензора деформации. Ведь именно скалярные инварианты тензора не зависят от системы координат. То есть 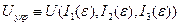(4.1.4)

Где , и далее, если не оговорено противное, тоU -упругая энергия. Разложим (4.1.4) в ряд Тейлора по аргументамI, сохраняя в этом разложении члены до второго порядка малости включительно и отбрасывая оставшуюся часть ряда

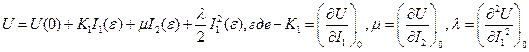(4.1.5)

Поскольку, согласно (4.1.2), напряжения есть производные упругой энергии по деформациям имеем: 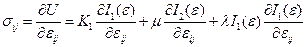, откуда после подстановки производных от инвариантов по деформациям

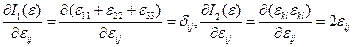получим 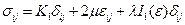. При нулевых деформациях должны быть нулевые напряжения, поэтому 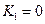. Окончательное выражение для компонент тензора напряжений в случае изотропной среды будет иметь следующий вид: 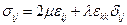, где λ, μ– постоянные Ламе(4.1.6)