Таким образом, как и в случае плоских волн, продольные волны несут изменение объема, а поперечные волны – изменение формы.

§ 5 . Волны в неограниченной анизотропной линейно-упругой среде.

Рассмотрев распространение малых возмущений в неограниченной изотропной, упругой среде, мы убедились в том, что в ней возможны волны только двух типов с продольной и поперечной поляризацией. Поскольку при распространении волн за период колебаний приток тепла практически равен нулю, т.е. процесс можно считать адиабатическим, именно упругие модули и плотность определяют скорость распространения волн в упругой среде. Как было показано выше, для анизотропного тела число упругих модулей равно 21. При наличии дополнительных симметрий, обусловленных физическими свойствами среды, количество независимых модулей уменьшается.

Выведем аналог уравнений Ламе в случае анизотропной упругой среды. Преобразуем правую часть уравнений движения ,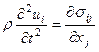

используя закон Гука в форме (4.1.3) и значения деформаций (1.4.13)

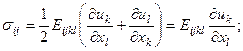
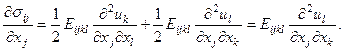
Тогда уравнения движения можно переписать в форме:

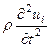
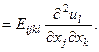(4.5.1)

Будем искать решение в форме бегущей плоской волны

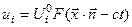, (4.5.2)

где 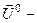вектор поляризации, 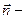нормаль к фронту волны, 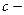фазовая скорость волн. Тогда получаем: .

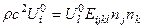Или, если ввести симметричный тензор Кристоффеля 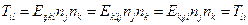, придем к уравнениям:

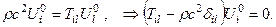(4.5.3)

Таким образом, величина 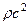является собственным значением введенного симметричного тензора второго ранга 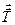, а векторы поляризации – соответственно будут собственными векторами этого тензора. Из общей теории следует, что для симметричного тензора существует три действительных собственных значения, а его собственные векторы ортогональны. Если мы покажем, что собственных значения положительны, то каждому собственному значению будет соответствовать своя фазовая скорость волн.

Для этого воспользуемся тем, что плотность упругой энергии 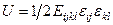является положительной величиной для любого симметричного тензора 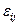. Произвольный тензор можно представить в виде суммы симметричного и антисимметричного тензоров

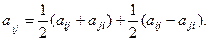
Если учесть, что свертка симметричного и антисимметричного тензора равна нулю и 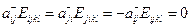, получим

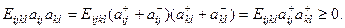(4.5.4)

Рассмотрим в качестве тензора 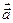тензор с компонентами 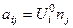. После умножения уравнения (4.5.3) на величину 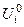и учета единичности вектора поляризации, получим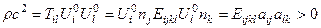

в силу неравенства (4.5.4).

Таким образом, можно считать доказанным, что в анизотропной среде есть три типа волн, скорость, которых определяется тензором упругих модулей и нормалью к фронту, поскольку тензор Кристоффеля 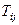зависит от нормали. В каждом направлении могут распространяться три волны с разными скоростями и ортогональными поляризациями. При этом вектор поляризации в общем случае не обязан совпадать с нормалью или быть перпендикулярным к ней, как это было для изотропной среды. Ту волну, для которой угол между вектором поляризации и вектором нормали является самым меньшим из трех, принято называть квазипродольной, а две другие волны квазипоперечными. Обычно квазипродольная волна является и самой быстрой. Для анизотропной среды, точечное возмущение приведет к возникновению несимметричных волновых фронтов, поскольку в каждом направлении, скорость волн будет иметь свое отличное от других направлений значение.