Абсолютное и относительное изменение уровней ряда
Система уровней ряда аналогична системе дискретных статистических величин X. По-прежнему вычисляются абсолютное, относительное изменения, среднее значение, а также соответствующие индексы и темпы изменения по единичным и средним значениям. Используются те же формулы средних величин от простой арифметической до геометрической.
Любое изменение уровней ряда определяется базисным и цепным способами.
Базисное абсолютное изменение представляет собой разность конкретного и первого уровней ряда, определяясь по формуле
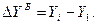(1.43)
Цепное абсолютное изменение представляет собой разность конкретного и предыдущего уровней ряда, определяясь по формуле
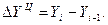(1.44)
По знаку абсолютного изменения делается вывод о характере развития явления: при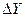 
> 0 — рост,при 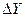< 0 — спад,при 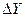= 0 — стабильность.
Для проверки правильности расчетов применяется правило, согласно которому сумма цепных абсолютных изменений равняется последнему базисному. То есть
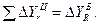(1.45)
где к = n-1 — количество изменений уровней ряда (r = 1 ...к).
Базисное относительное изменение представляет собой соотношение конкретного и первого уровней ряда, определяясь по формуле
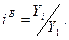(1.46)
Цепное относительное изменение представляет собой соотношение конкретного и предыдущего уровней ряда, определяясь по формуле
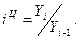(1.47)
Относительные изменения уровней — это по существу индексы динамики, критериальным значением которых служит 1. Если они больше ее, имеет место ростявления, меньше ее — спад,а при равенстве единице наблюдается стабильностьявления.
Вычитая единицу из относительных изменений, получают темп изменения уровней, критериальным значением которого служит 0. При положительном темпе изменения имеет место ростявления, при отрицательном — спад,а при нулевом темпе изменения наблюдается стабильностьявления.
Для проверки правильности расчетов применяется правило, согласно которому произведение цепных относительных изменений равняется последнему базисному.
То есть
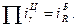(1.48)
Дата добавления: 2015-12-26; просмотров: 1807;