Средний уровень ряда и средние изменения
Способ расчета среднего уровня зависит от того, моментный ряд или интервальный. При моментном ряде применяется формула средней хронологической величины (1.17), но при соответствующих обозначениях имеющая вид
= 
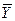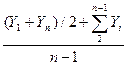, (1.49)
где Y1 и Yn — первый и последний уровни ряда; Yi — промежуточные уровни.
В случае интервального ряда его средний уровень определяется по формуле простой средней арифметической величины как
= 
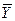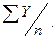(1.50)
Среднее изменение уровней ряда определяется также базисным и цепным способами.
Базисное среднее абсолютное изменение представляет собой частное от деления последнего базисного абсолютного изменения на количество изменений. То есть
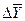Б = 
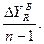(1.51)
Цепное среднее абсолютное изменение уровней ряда представляет собой частное от деления суммы всех цепных абсолютных изменений наколичество изменений.
То есть 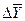Ц =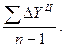 
(1.52)
По знаку средних абсолютных изменений также судят о характере изменения явления в среднем: рост, спад или стабильность.
Из правила контроля базисных и цепных абсолютных изменений согласно формуле (1.45) следует, что базисное и цепное среднее изменение должны быть равными.
Наряду со средними абсолютным изменением рассчитывается и среднее относительное тоже базисным и цепным способами.
Базисное среднее относительное изменение определяется по формуле
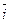Б=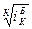 
= 
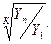(1.53)
Цепное среднее относительное изменение определяется по формуле
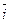Ц=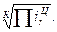 
(1.54)
Естественно, базисное и цепное среднее относительное изменения должны быть одинаковыми и сравнением их с критериальным значением 1 делается вывод о характере изменения явления в среднем: рост, спад или стабильность.
Вычитанием 1 из базисного или цепного среднего относительного изменения образуется соответствующий средний темп изменения, по знаку которого также можно судить о характере изменения изучаемого явления, отраженного данным рядом динамики.
Дата добавления: 2015-12-26; просмотров: 873;