Предельная ошибка выборки
Учитывая, что на основе выборочного обследования нельзя точно оценить изучаемый параметр (например, среднее значение) генеральной совокупности, необходимо найти пределы, в которых он находится. В конкретной выборке разность 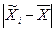 может быть больше, меньше или равна
может быть больше, меньше или равна 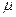 . Каждое из отклонений
. Каждое из отклонений 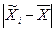 от
от 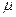 имеет определенную вероятность. При выборочном обследовании реальное значение
имеет определенную вероятность. При выборочном обследовании реальное значение 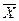 в генеральной совокупности неизвестно. Зная среднюю ошибку выборки, с определенной вероятностью можно оценить отклонение выборочной средней от генеральной и установить пределы, в которых находится изучаемый параметр (в данном случае среднее значение) в генеральной совокупности. Отклонение выборочной характеристики от генеральной называется предельной ошибкой выборки
в генеральной совокупности неизвестно. Зная среднюю ошибку выборки, с определенной вероятностью можно оценить отклонение выборочной средней от генеральной и установить пределы, в которых находится изучаемый параметр (в данном случае среднее значение) в генеральной совокупности. Отклонение выборочной характеристики от генеральной называется предельной ошибкой выборки 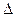 . Она определяется в долях средней ошибки с заданной вероятностью, т.е.
. Она определяется в долях средней ошибки с заданной вероятностью, т.е.
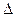 = t
= t 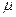 ,(1.38)
,(1.38)
где t – коэффициент доверия, зависящий от вероятности, с которой определяется предельная ошибка выборки.
Вероятность появления определенной ошибки выборки находят с помощью теорем теории вероятностей. Согласно теореме П. Л. Чебышёва, при достаточно большом объеме выборки и ограниченной дисперсии генеральной совокупности вероятность того, что разность между выборочной средней и генеральной средней будет сколь угодно мала, близка к единице:
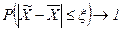 при
при 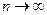 .
.
А. М. Ляпунов доказал, что независимо от характера распределения генеральной совокупности при увеличении объема выборки распределение вероятностей появления того или иного значения выборочной средней приближается к нормальному распределению. Это так называемая центральная предельная теорема. Следовательно, вероятность отклонения выборочной средней от генеральной средней, т.е. вероятность появления заданной предельной ошибки, также подчиняется указанному закону и может быть найдена как функция от t с помощью интеграла вероятностей Лапласа:
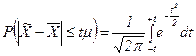 ,
,
где 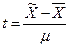 – нормированное отклонение выборочной средней от генеральной средней.
– нормированное отклонение выборочной средней от генеральной средней.
Значения интеграла Лапласа для разных t рассчитаны и имеются в специальных таблицах, из которых в статистике широко применяется сочетание:
| Вероятность | 0,683 | 0,866 | 0,950 | 0,954 | 0,988 | 0,990 | 0,997 | 0,999 |
| t | 1,5 | 1,96 | 2,5 | 2,58 | 3,5 |
Задавшись конкретным уровнем вероятности, выбирают величину нормированного отклонения t и определяют предельную ошибку выборки по формуле (1.38)
При этом чаще всего применяют 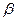 = 0,95 и t = 1,96, т.е. считают, что с вероятностью 95% предельная ошибка выборки вдвое больше средней. Поэтому в статистике величина t иногда именуется коэффициентом кратности предельной ошибки относительно средней.
= 0,95 и t = 1,96, т.е. считают, что с вероятностью 95% предельная ошибка выборки вдвое больше средней. Поэтому в статистике величина t иногда именуется коэффициентом кратности предельной ошибки относительно средней.
После исчисления предельной ошибки находят доверительный интервал обобщающей характеристики генеральной совокупности. Такой интервал для генеральной средней величины имеет вид
( 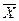 -
- 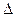 )
) 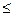
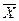
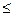 (
( 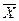 +
+ 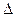 ),(1.39)
),(1.39)
адля генеральной доли аналогично
(w- 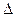 )
) 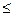 p
p 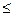 (w +
(w + 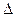 ).(1.40)
).(1.40)
Следовательно, при выборочном наблюдении определяется не одно, точное значение обобщающей характеристики генеральной совокупности, а лишь ее доверительный интервал с заданным уровнем вероятности. И это серьезный недостаток выборочного метода статистики.
Дата добавления: 2015-12-26; просмотров: 1165;
