Средняя ошибка выборки
Выборочную совокупность можно сформировать по количественному признаку статистических величин, а также по альтернативному или атрибутивному. В первом случае обобщающей характеристикой выборки служит выборочная средняя величина, обозначаемая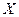 
, а во втором — выборочная доля величин, обозначаемая w. В генеральной совокупности соответственно: генеральная средняя 
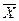и генеральная доля р .
Разности 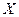— 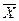и W — р называются ошибкой выборки, которая делится на ошибку регистрации и ошибку репрезентативности. Первая часть ошибки выборки возникает из-за неправильных или неточных сведений по причинам непонимания существа вопроса, невнимательности регистратора при заполнении анкет, формуляров и т.п. Она достаточно легко обнаруживается и устраняется. Вторая часть ошибки возникает из-за постоянного или спонтанного несоблюдения принципа случайности отбора. Ее трудно обнаружить и устранить, она гораздо больше первой и потому ей уделяется основное внимание.
Величина ошибки выборки зависит от структуры последней. Например, если при определении среднего балла успеваемости студентов факультета в одну выборку включить больше отличников, а в другую - больше неудачников, то выборочные средние баллы и ошибки выборки будут разными.
Поэтому в статистике определяется средняя ошибка повторной и бесповторной выборки в виде ее удельного среднего квадратического отклонения по формулам
= 
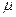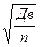- повторная; (1.35)
= 
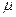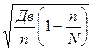- бесповторная; (1.36)
где Дв — выборочная дисперсия, определяемая при количественном признаке статистических величин по обычным формулам из гл.2.
При альтернативном или атрибутивном признаке выборочная дисперсия определяется по формуле
Дв = w(1-w).(1.37)
Из формул (1.35) и (1.36) видно, что средняя ошибка меньше у бесповторной выборки, что и обусловливает ее более широкое применение.
Дата добавления: 2015-12-26; просмотров: 854;