Выборки и доверительные интервалы
Пусть у нас имеется большое количество предметов, с нормальным распределением некоторых характеристик (например, полный склад однотипных овощей, размер и вес которых варьируется). Вы хотите знать средние характеристики всей партии товара, но у Вас нет ни времени, ни желания измерять и взвешивать каждый овощ. Вы понимаете, что в этом нет необходимости. Но сколько штук надо было бы взять на выборочную проверку?
Прежде, чем дать несколько полезных для этой ситуации формул напомним некоторые обозначения.
Во-первых, если бы мы все-таки промерили весь склад овощей (это множество элементов называется генеральной совокупностью), то мы узнали бы со всей доступной нам точностью среднее значение веса всей партии. Назовем это среднее значение Хср.ген. - генеральным средним. Мы уже знаем, что нормальное распределение определяется полностью, если известно его среднее значение и отклонение s . Правда, пока мы ни Хср.ген., ни sгенеральной совокупности не знаем. Мы можем только взять некоторую выборку, замерить нужные нам значения и посчитать для этой выборки как среднее значение Хср.выб., так и среднее квадратическое отклонение Sвыб.
Известно, что если наша выборочная проверка содержит большое количество элементов (обычно n больше 30), и они взяты действительно случайным образом, то s генеральной совокупности почти не будет отличаться от Sвыб
Кроме того, для случая нормального распределения мы можем пользоваться следующими формулами:
С вероятностью 95%
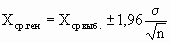
С вероятностью 99%

Дата добавления: 2015-12-22; просмотров: 749;
