Доверительные интервалы.

Вычисление доверительного интервала базируется на средней ошибке соответствующего параметра. Доверительный интервал показывает, в каких пределах с вероятностью (1-a) находится истинное значение оцениваемого параметра. Здесь a – уровень значимости, (1-a) называют также доверительной вероятностью.

В первой главе мы показали, что, например, для среднего арифметического, истинное среднее по сово­купности примерно в 95% случаев лежит в пределах 2 средних ошибок среднего. Таким образом, границы 95% доверительного интервала для среднего будет отстоять от выборочного среднего на удвоенную среднюю ошибку среднего, т.е. мы умножаем среднюю ошибку среднего на некий коэффициент, зависящий от доверительной вероятности. Для среднего и разности средних берётся коэффициент Стьюдента (критическое значение критерия Стьюдента), для доли и разности долей критическое значение критерия z. Произведение коэффициента на среднюю ошибку можно назвать предельной ошибкой данного параметра, т.е. максимальную, которую мы можем получить при его оценке.

Далее приведены формулы для расчёта доверительных интервалов для среднего, разности средних, доли и разности долей.

Доверительный интервал для среднего арифметического: .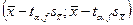

Здесь 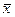- выборочное среднее;

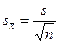- средняя ошибка среднего арифметического;

s – выборочное среднее квадратическое отклонение;

n – объём выборки (численность группы);

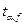- критическое значение критерия Стьюдента при заданных уровне значимости a и числе степеней свободы f = n-1 (коэффициент Стьюдента).

Доверительный интервал для разности средних арифметических:

.

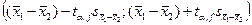Здесь 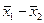- разность выборочных средних;

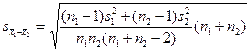- средняя ошибка разности средних арифметических;

s₁,s₂ – выборочные средние квадратические отклонения;

n₁,n₂ – объёмы выборок (численности групп);

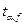- критическое значение критерия Стьюдента при заданных уровне значимости a и числе степеней свободы f=n₁+n₂-2 (коэффициент Стьюдента).

Доверительный интервал для доли:

.

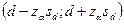Здесь d – выборочная доля;

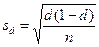– средняя ошибка доли;

n – объём выборки (численность группы);

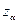- критическое значение критерия z при заданном уровне значимости a ( , , ).

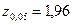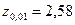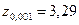Доверительный интервал для разности долей:

.

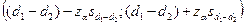Здесь 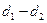- разность выборочных долей;

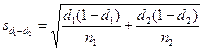– средняя ошибка разности средних арифметических;

n₁,n₂ – объёмы выборок (численности групп);

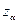- критическое значение критерия z при заданном уровне значимости a ( , , ).

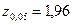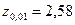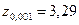Вычисляя доверительные интервалы для разности показателей, мы, во-первых, непосредственно видим возможные значения эффекта, а не только его точечную оценку. Во-вторых, можем сделать вывод о принятии или опровержении нулевой гипотезы и, в-третьих, можем сделать вывод о мощности критерия.

При проверке гипотез с помощью доверительных интервалов надо придерживаться следующего правила:

Если 100(1-a)-процентный доверительный интервал разности средних не содержит нуля, то различия статистически значимы на уровне значимости a; напротив, если этот интервал содержит ноль, то различия статистически не значимы.

Действительно, если этот интервал содержит ноль, то, значит, сравниваемый показатель может оказаться как больше, так и меньше в одной из групп, по сравнению с другой, т.е. наблюдаемые различия случайны.

По месту, где находится ноль внутри доверительного интервала, можно судить о мощности критерия. Если ноль близок к нижней или верхней границе интервала, то возможно при большей численности сравниваемых групп, различия достигли бы статистической значимости. Если ноль близок к середине интервала, то, значит, равновероятно и увеличение и уменьшение показателя в экспериментальной группе, и, вероятно, различий действительно нет.

Примеры:

Сравнить операционную летальность при применении двух разных видов анестезии: с применением первого вида анестезии оперировалось 61 человек, умерло 8, с применением второго – 67 человек, умерло 10.

d₁ = 8/61 = 0,131; d₂ = 10/67 = 0,149; d1-d2 = - 0,018.

.

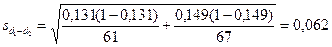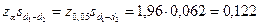
Разность летальностей сравниваемых методов будет находиться в интервале (-0,018 - 0,122; -0,018 + 0,122) или (-0,14 ; 0,104) с вероятностью 100(1-a) = 95%. Интервал содержит ноль, т.е. гипотезу об одинаковой летальности при двух разных видах анестезии отвергнуть нельзя.

Таким образом, летальность может и уменьшится до 14% и увеличиться до 10,4% с вероятностью 95%, т.е. ноль находится примерно по середине интервала, поэтому можно утверждать, что, скорее всего, действительно не отличаются по летальности эти два метода.

В рассмотренном ранее примере сравнивалось среднее время нажатия при теппинг-тесте в четырёх группах студентов, отличающихся по экзаменационной оценке. Вычислим доверительные интервалы среднего времени нажатия для студентов, сдавших экзамен на 2 и на 5 и доверительный интервал для разности этих средних.

Коэффициенты Стьюдента находим по таблицам распределения Стьюдента (см. приложение): для первой группы: 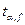= t(0,05;48) = 2,011; для второй группы: 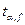= t(0,05;61) = 2,000. Таким образом, доверительные интервалы для первой группы: 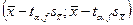= (162,19-2,011*2,18 ; 162,19+2,011*2,18) = (157,8 ; 166,6) , для второй группы (156,55-2,000*1,88 ; 156,55+2,000*1,88) = (152,8 ; 160,3). Итак, для сдавших экзамен на 2, среднее время нажатия лежит в пределах от 157,8 мс до 166,6 мс с вероятностью 95%, для сдавших экзамен на 5 – от 152,8 мс до 160,3 мс с вероятностью 95%.

Проверять нулевую гипотезу можно и по доверительным интервалам для средних, а не только для разности средних. Например, как в нашем случае, если доверительные интервалы для средних перекрываются, то нулевую гипотезу отвергнуть нельзя. Для того чтобы отвергнуть гипотезу на выбранном уровне значимости, соответствующие доверительные интервалы не должны перекрываться.

Найдём доверительный интервал для разности среднего времени нажатия в группах сдавших экзамен на 2 и на 5. Разность средних: 162,19 – 156,55 = 5,64. Коэффициент Стьюдента: 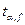= t(0,05;49+62-2) = t(0,05;109) = 1,982. Групповые средние квадратические отклонения будут равны: 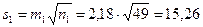; 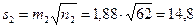. Вычисляем среднюю ошибку разности средних: 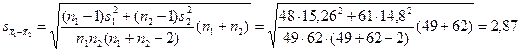. Доверительный интервал: 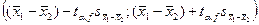=(5,64-1,982*2,87 ; 5,64+1,982*2,87) = (-0,044 ; 11,33).

Итак, разница среднего времени нажатия в группах, сдавших экзамен на 2 и на 5, будет находиться в интервале от -0,044 мс до 11,33 мс. В этот интервал входит ноль, т.е. среднее время нажатия у отлично сдавших экзамен, может и увеличиться и уменьшится по сравнению с неудовлетворительно сдавшими, т.е. нулевую гипотезу отвергнуть нельзя. Но ноль находится очень близко к нижней границе, время нажатия гораздо вероятнее всё-таки уменьшается у отлично сдавших. Таким образом, можно сделать вывод, что различия в среднем времени нажатия между сдавшими на 2 и на 5 всё-таки есть, просто мы не смогли их обнаружить при данном изменении среднего времени, разбросе среднего времени и объёмах выборок.

ВЫВОДЫ.

Мощность критерия – это вероятность отвергнуть неверную нулевую гипотезу, т.е. найти различия там, где они действительно есть.

Мощность критерия определяется исходя из уровня значимости, величины различий между группами, разброса значений в группах и объёма выборок.

Для критерия Стьюдента и дисперсионного анализа можно воспользоваться диаграммами чувствительности.

Мощность критерия можно использовать при предварительном определении необходимой численности групп.

Доверительный интервал показывает, в каких пределах с заданной вероятностью находится истинное значение оцениваемого параметра.

С помощью доверительных интервалов можно проверять статистические гипотезы и делать выводы о чувствительности критериев.

ЛИТЕРАТУРА.

Гланц С. – Глава 6,7.

Реброва О.Ю. – с.112-114, с.171-173, с.234-238.

Сидоренко Е. В. – с.32-33.

Вопросы для самопроверки студентов.

1. Что такое мощность критерия?

2. В каких случаях необходимо оценить мощность критериев?

3. Способы расчёта мощности.

4. Как рассчитать необходимую численность групп при заданной мощности?

5. Как рассчитать доверительные интервалы для средних, разности средних, долей, разности долей?

6. Как проверить статистическую гипотезу с помощью доверительного интервала?

7. Что можно сказать о мощности критерия при расчёте доверительного интервала?

Задачи.

№3, 5, 7, 12, 15, 21.