Сравнение двух групп. Критерий Вилкоксона.
Порядок расчёта.
1. Вычислить величины изменений наблюдаемого признака. Отбросить пары с нулевым изменением.
2. Упорядочить изменения по возрастанию их абсолютной величины и присвоить ранги (совпадающим значениям присваивается средний ранг мест, которые они занимают).
3. Присвоить рангу знак в соответствии с изменением: «+» - увеличилось, «-» - уменьшилось.
4. Вычислить сумму рангов с учётом знака. Это и будет экспериментальное значение критерия Вилкоксона W.
5. Экспериментальное значение сравнивается с критическим, определяемым по соответствующим статистическим таблицам, исходя из требуемого уровня значимости и численности групп. В приложениях приведены значения для численности групп не превосходящей 20.
Если число пар измерений больше 20, то распределение W достаточно близко к нормальному со средним 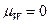 и средним квадратическим отклонением
и средним квадратическим отклонением
 ,
,
где n – число пар наблюдений (численность группы).
Если некоторые значения совпадают, то среднее квадратическое отклонение должно уменьшится в соответствии со следующей формулой:
 ,
,
где  - число значений i-го совпадающего ранга.
- число значений i-го совпадающего ранга.
Можно, таким образом, использовать в качестве экспериментального значения:
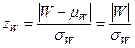 или с поправкой Йейтса на непрерывность
или с поправкой Йейтса на непрерывность
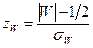 , которое сравнивается с критическими значениями:
, которое сравнивается с критическими значениями: 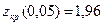 ,
, 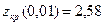 ,
,  .
.
Пример 4:
Рассмотрим задачу, которую мы решили для зависимых выборок с помощью парного критерия Стьюдента. У него есть ограничение на нормальное распределение изменений. У критерия Вилкоксона таких ограничений нет, и его можно применять и для количественных переменных, если нет достаточных оснований для нормальности изменений признака.
| До | После | Изменение | Ранг | Знаковый ранг |
| 3,5 | 3,5 | |||
| 8,5 | 8,5 | |||
| 3,5 | 3,5 | |||
| -1 | -1 | |||
| 8,5 | 8,5 | |||
| Сумма |
Итак, экспериментальное значение критерия Вилкоксона равно W = 64.
Критическое значение по таблице равно  .
.
Таким образом, экспериментальное значение больше критического и нулевая гипотеза об отсутствии влияния курения на агрегацию тромбоцитов отвергается с вероятностью ошибки меньше 0,018.
Дата добавления: 2016-02-04; просмотров: 936;
