Мощность критериев.

Как правило, вспоминают о мощности критерия, когда различия не выявлены, т.е. при проверке гипотезы получен результат, что нулевую гипотезу нельзя отвергнуть. Напоминаем, что чувствительность или мощность критерия это вероятность найти различия там, где они действительно есть. Поэтому если мы не нашли различия, желательно оценить мощность критерия в данном случае. Если она высокая (более 75%), то, скорее всего, различий действительно нет. Однозначный такой вывод можно сформулировать, только если мощность равна 100%. Если же мощность критерия мала, то различия возможно на самом деле есть, но мы не смогли их доказать.

На мощность критерия влияет:

- уровень значимости (чем с меньшей вероятностью ошибки мы хотим доказать различия, тем с большей вероятностью мы не найдём их там, где они действительно есть);

- величина различий (разница между сравниваемыми параметрами);

- разброс значений (среднее квадратическое отклонение);

- объём выборки.

Для оценки мощности критерия Стьюдента можно воспользоваться диаграммами чувствительности (рис.1). На них мощность определяется как функция параметра нецентральности при заданном объёме выборки (численности сравниваемых групп) и заданном уровне значимости (обычно минимальный a=0,05).

Параметр нецентральности j определяется как отношение разницы сравниваемых средних d к среднему квадратическому отклонению изучаемого параметра в генеральной совокупности s: .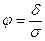

В качестве s при расчётах берётся объединённая оценка среднего квадратического ототклонения: .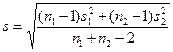

Пример:

В примере, рассмотренном при сравнении групп больных по частоте пульса с помощью критерия Стьюдента мы не выявили различий. Оценим мощность критерия при этих данных.

Измерения пульса 10 больных, проведенные после некоторой процедуры, и 12 больных контрольной группы дали следующие результаты: для I группы 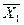= 70 уд/мин, для II группы 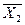= 68 уд/мин; оценки дисперсий соответственно равны: 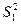= 9 (уд/мин)², и 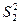= 4 (уд/мин)².

Разница средних: 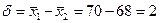(уд/мин).

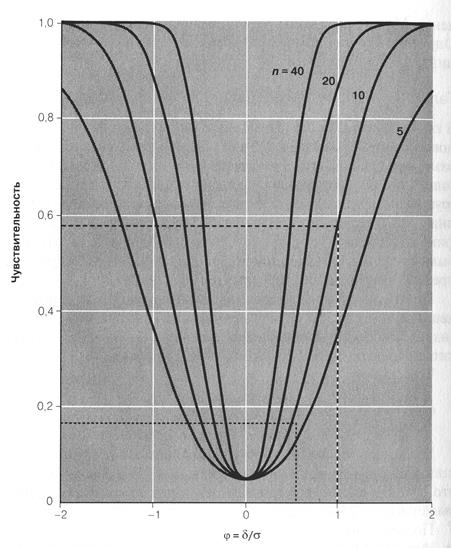
Рис. 1. Чувствительность (мощность) критерия Стьюдента как функция от параметра нецентральности j при уровне значимости a = 0,05 для разных объёмов выборок n.

Объединённая оценка среднего квадратического отклонения:

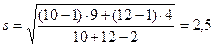(уд/мин).

Параметр нецентральности: .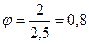

При уровне значимости a=0,05 и численности групп 10 (при неодинаковой численности берётся меньшее значение) мощность критерия Стьюдента по диаграмме (рис.1) составляет 40%. Мощность недостаточно высокая, можно утверждать, что на самом деле процедура оказывает действие на пульс, просто мы этого не выявили. Для доказательства эффективности процедуры можно попытаться проверить гипотезу непараметрическим методом или, что гораздо лучше, увеличить численность групп и заново провести сравнение. Например, если мы увеличим численность сравниваемых групп до 20 человек, то при тех же остальных параметрах мощность составит уже 75%, т.е. гораздо более вероятнее сумеем найти различия.

Для оценки мощности дисперсионного анализа также можно воспользоваться диаграммами [Гланц С., приложение Б]. Параметр нецентральности в этом случае можно рассчитать двумя способами:

1) ,

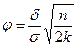где k – количество сравниваемых групп;

n – численность каждой из групп (если неодинаковы, то берём наименьшее значение);

s – среднее квадратическое отклонение в совокупности, в качестве которой берём объединённую оценку 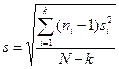, n_i – численность i-ой группы; s_i – среднее квадратическое отклонение в i-ой группе, 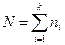- общая численность обследованных;

2) ,

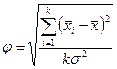где 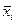– среднее в i-ой группе;

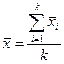- среднее по всем группам.

Мощность критерия можно использовать при планировании эксперимента, т.е. предварительного определения необходимой численности групп. В этом случае мы задаёмся достаточной мощностью и примерно оценив параметр нецентральности, например, по данным литературы или по предварительному исследованию, определяем необходимую численность группы. Это может быть очень полезно, чтобы не проводить заведомо несостоятельные исследования.

Оценка чувствительности довольно сложная задача, особенно при сравнении качественных признаков. Для формулирования вывода при не отвержении нулевой гипотезы, действительно нет различий или мы их просто не нашли можно воспользоваться доверительными интервалами для разницы сравниваемых величин. С помощью доверительных интервалов можно и вообще проверять нулевую гипотезу.