Метод свертывания критериев.
В методах, основанных на свертывании критериев, из локальных критериев формируется один. Наиболее распространенным является метод линейной комбинации частных критериев. Пусть задан вектор весовых коэффициентов критериев 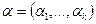 , характеризующих важность соответствующего критерия,
, характеризующих важность соответствующего критерия, 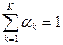 ,
, 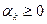
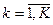 . Линейная скаляризованная функция представляет собой сумму частных критериев, умноженных на весовые коэффициенты. Задача математического программирования становится однокритериальной и имеет вид
. Линейная скаляризованная функция представляет собой сумму частных критериев, умноженных на весовые коэффициенты. Задача математического программирования становится однокритериальной и имеет вид
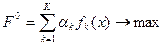
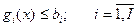 ;
;
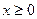 .
.
Критерии в свертке должны быть нормированы.
К недостаткам метода можно отнести то, что малым приращениям коэффициентов соответствуют большие приращения функции, т. е. решение задачи неустойчиво, а также необходимость определения весовых коэффициентов.
В [3] приведен сравнительный анализ методов определения коэффициентов важности критериев, в котором отмечено, что наиболее простой прием для определения весов в аддитивной свертке предложил
Х. Юттлер, где в качестве весовых коэффициентов используются величины, обратные оптимальным значениям по частным критериям:
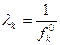 ,
,
где 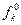 - оптимальное максимальное значение критерия
- оптимальное максимальное значение критерия 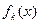 .
.
Дата добавления: 2016-01-20; просмотров: 3295;
